Convolutional Neural Networks
概述
在普通的深度神经网络(DNN)中,每个单元都可看做是一个神经元,每一层的神经元都会接受来自上一层所有神经元的信号;句话说,前一层即使只有一个神经元是兴奋的,它也会激活后面所有层的所有神经元。这种人工神经网络设计并不符合生物神经学,生物学家发现动物在接收不同的刺激时,大脑中活跃的区域是不一样的,这就说明神经元之间并不是全连接(Fully Connected)关系,而是一种选择性连接的关系。这就是卷积神经网络(Convolutional Neural Networks)诞生的起源。
CNN最初也是最广泛应用的领域就是图像处理,假设有一张$32{\times}32$的RGB图片,再假设眼球的神经元能看到的范围为$5{\times}5$,并且能接受RGB信号,那么会有类似如下的结构:

$32{\times}32{\times}3$表示的是输入卷积网络的图片,$5{\times}5{\times}3$的filter也被称为卷积网络的卷积核,用于提取图片的区域特征。CNN使用卷积核去扫描图片,每扫描一个区域会得到一个输出信号,那么该图片经过卷积核的扫描之后会得到一个信号矩阵:
具体过程见下图(图源百度):
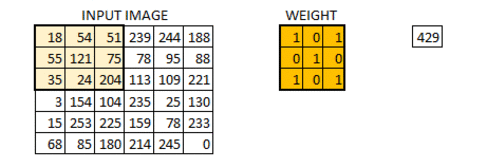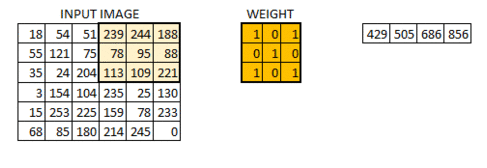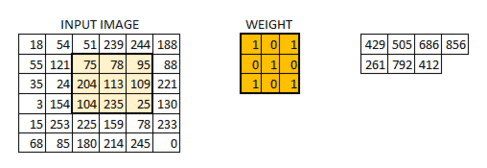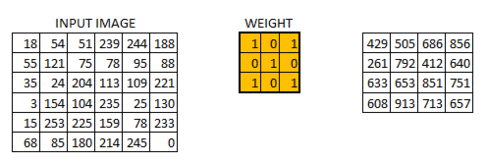
信号矩阵在经过激活函数激活之后会得到一个激活矩阵,这一处理过程被称为激活映射(Active Mapping)。使用一个卷积核会得到一个激活矩阵,那么使用多个卷积核会得到多个激活矩阵,即该层网络的输出,也是下层网络的输入:

在CNN中,执行激活映射的层被称为卷积层(Convolution Layer)。设输入尺寸为$nn$,卷积核的尺寸为$k$,那么卷积层的输出为$n-k+1$。卷积核还有一个可设定的参数,步长(stride),该参数指明卷积核每次扫描移动的行列数,在该参数设定的条件下,卷积核的输出尺寸为$(n-k)/s+1$。经过若干卷积层之后,网络中数据的尺寸是越来越小的:
为了防止数据尺寸缩小的太快,CNN会使用一种padding的技术,对数据的边缘填充0值来增大输入数据的尺寸,那么在使用padding技术时的输出尺寸为:
\[o=(n+2p-k)/s+1\]除了卷积层,CNN中还有池化层(Pooling Layer)。池化层的目的很简单,就是对数据做降采样(downsampling)。上面提到不使用padding的卷积层会使数据尺寸变小,对应的,在池化层中,不使用padding,并且设置较大的stride来达到数据缩减的目的。最常见的池化方法有平均池化与最大化池化。下图为最大化池化的示例(图源百度):
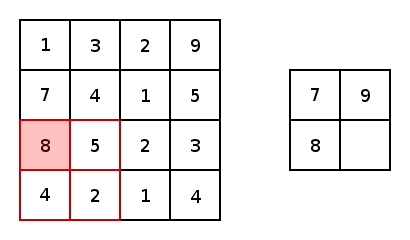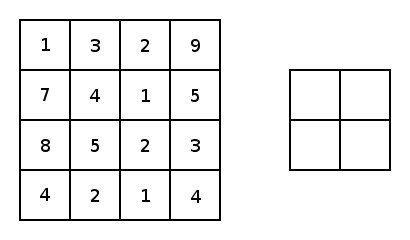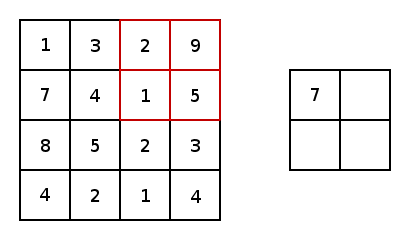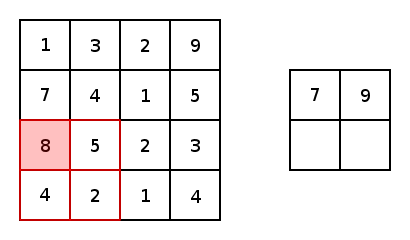
一个完整的CNN包含若干个卷积层与池化层,最后是全连接层。注意只有卷积层才有激活函数。
训练
CNN中的卷积核相当于DNN中的权重矩阵,那么CNN中的参数即是卷积核张量。一个尺寸为$k{\times}k{\times}d$的卷积核,其中的参数数量为:
\[k{\times}k{\times}d+1\]其中$+1$表示的是bias。
一个简单的CNN实现指导见此。
CNN Architectures
最初始的CNN架构应该是LeNet-5,关于该网络的实现见此。
AlexNet
AlexNet算是首个成功的CNN结构,其在2012年的ImageNet图像分类比赛中获得冠军。其网络结构如下所示:

| Input | kernel num | kernel size | stride | pad | Output | |
|---|---|---|---|---|---|---|
| Conv1 | $227{\times}227{\times}3$ | $96$ | $11{\times}11$ | 4 | 0 | $(227-11)/4+1$ |
| MaxPool1 | $55{\times}55{\times}96$ | - | $3{\times}3$ | 2 | - | $(55-3)/2+1$ |
| Norm1 | $27{\times}27{\times}96$ | - | - | - | - | 27 |
| Conv2 | $27{\times}27{\times}96$ | $256$ | $5{\times}5$ | 1 | 2 | $(27+2{\times}2-5)/1+1$ |
| MaxPool2 | $27{\times}27{\times}256$ | - | $3{\times}3$ | 2 | - | $(27-3)/2+1$ |
| Norm2 | $13{\times}13{\times}256$ | - | - | - | - | 27 |
| Conv3 | $13{\times}13{\times}256$ | $384$ | $3{\times}3$ | 1 | 1 | $(13+2{\times}1-3)/1+1$ |
| Conv4 | $13{\times}13{\times}384$ | $384$ | $3{\times}3$ | 1 | 1 | $(13+2{\times}1-3)/1+1$ |
| Conv5 | $13{\times}13{\times}384$ | $256$ | $3{\times}3$ | 1 | 1 | $(13+2{\times}1-3)/1+1$ |
| MaxPool3 | $13{\times}13{\times}256$ | - | $3{\times}3$ | 2 | - | $(13-3)/2+1$ |
| FC6 | $6{\times}6{\times}256$ | 4096 | - | - | - | $1{\times}4096$ |
| FC7 | $1{\times}4096$ | 4096 | - | - | - | $1{\times}4096$ |
| FC8 | $1{\times}4096$ | 1000 | - | - | - | $1{\times}1000$ |
AlexNet有几个关键点:
- 首次在实践中使用ReLU作为激活函数
- 使用了归一化层来做局部归一化(LRN)
- 使用dropout技术避免过拟合
- 做了大量的数据增强(图像翻转、旋转)
- 全部使用最大池化,并且池化核的步长小于核大小,使池化核之间有重叠
- 使用两个GPU并行训练
- 使用带动量的SGD,当损失不再下降时手动将学习率除以10
VGG
VGG是2014年ImageNet图像分类挑战的亚军,其扩展了AlexNet的结构,使用了更深层的神经网络模型来达到更好的效果。下图是VGG16的网络结构图:

VGG中只使用了两种核:
| kernel size | stride | padding | |
|---|---|---|---|
| Conv Kernel | $3{\times}3$ | $1$ | $1$ |
| MaxPooling Kernel | $2{\times}2$ | $2$ | - |
易得VGG中的卷积层不改变数据的尺寸,但是会增加数据的深度;而最大池化层每次都会将数据的尺寸减半,但深度不变。这样一来,数据在VGG中传递时尺寸不断减小,深度不断增加,自然地过渡到一个一维向量(预测输出)。
并且级联的小核卷积层相当于一个单个的大核卷积层,但是参数数量却大大降低。假设输入图片维度为$(7,7,3)$,在经过两个使用$3{\times}3{\times}3$卷积核的级联卷积层后,数据流维度变为$(3,3,3)$,而两层六个卷积核的参数数量为:$6{\times}3{\times}3{\times}3=162$;假设把两层小核卷积层换成一个使用$5{\times}5{\times}3$卷积核的卷积层,输出数据流维度同样为$(3,3,3)$,那么三个大卷积核的参数数量为:$3{\times}5{\times}5{\times}3=225$。除了减小参数数量之外,增加的卷积层为神经网络增加了更多的非线性因素。
接下来分析VGG16各层需要的内存量(数据流占用内存)与参数数量:
| layer | mem | param |
|---|---|---|
| Input | $224{\times}224{\times}3=150K$ | 0 |
| Conv1-1 | $224{\times}224{\times}64=3.2M$ | $64{\times}3{\times}3{\times}3$ |
| Conv1-2 | $224{\times}224{\times}64=3.2M$ | $64{\times}3{\times}3{\times}64$ |
| MaxPool1 | $112{\times}112{\times}64=800K$ | 0 |
| Conv2-1 | $112{\times}112{\times}128=1.6M$ | $128{\times}3{\times}3{\times}64$ |
| Conv2-2 | $112{\times}112{\times}128=1.6M$ | $128{\times}3{\times}3{\times}128$ |
| MaxPool2 | $56{\times}56{\times}128=400K$ | 0 |
| Conv3-1 | $56{\times}56{\times}256=800K$ | $256{\times}3{\times}3{\times}128$ |
| Conv3-2 | $56{\times}56{\times}256=800K$ | $256{\times}3{\times}3{\times}256$ |
| Conv3-3 | $56{\times}56{\times}256=800K$ | $256{\times}3{\times}3{\times}256$ |
| MaxPool3 | $28{\times}28{\times}256=200K$ | 0 |
| Conv4-1 | $28{\times}28{\times}512=400K$ | $512{\times}3{\times}3{\times}256$ |
| Conv4-2 | $28{\times}28{\times}512=400K$ | $512{\times}3{\times}3{\times}512$ |
| Conv4-3 | $28{\times}28{\times}512=400K$ | $512{\times}3{\times}3{\times}512$ |
| MaxPool4 | $14{\times}14{\times}512=100K$ | 0 |
| Conv5-1 | $14{\times}14{\times}512=100K$ | $512{\times}3{\times}3{\times}512$ |
| Conv5-2 | $14{\times}14{\times}512=100K$ | $512{\times}3{\times}3{\times}512$ |
| Conv5-3 | $14{\times}14{\times}512=100K$ | $512{\times}3{\times}3{\times}512$ |
| MaxPool5 | $7{\times}7{\times}512=25K$ | 0 |
| FC6 | $1{\times}4096=4K$ | $7{\times}7{\times}512{\times}4096=98M$ |
| FC7 | $1{\times}4096=4K$ | $4096{\times}4096=16M$ |
| FC8 | $1{\times}1000=1K$ | $4096{\times}1000=4M$ |
根据以上表格,发现计算时的最大内存开销在于前面两层卷积层,而参数的数量绝大部分都在全连接层。以每一个数字占$32$bit来算,仅计算一张图片在VGG中的前向传播过程就至少需要$60$MB的内存,保存VGG模型的所有参数至少需要$526$MB的存储空间。
一个不完整的VGG实现示例见这里。完整预训练的VGG16模型重载见这里。
GoogLeNet
GoogLeNet是2014年ImageNet图像分类挑战的冠军,它同样扩展了AlexNet的网络深度,但不同于VGG,GoogLeNet使用了一种全新的网络子结构来减少参数与运算量。
Interception Module
Interception Module是GoogLeNet中出现的全新网络子结构,如下图所示:
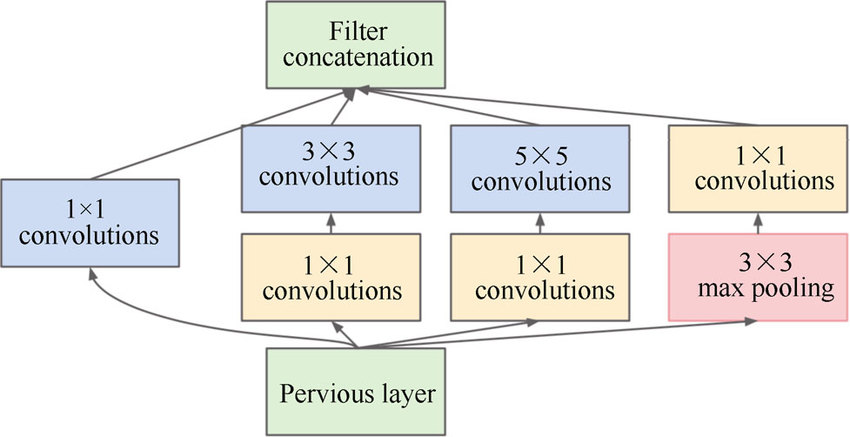
一个Interception Module对上一层的输出并行地做了三次基于不同卷积核的卷积运算与一次池化运算,并且引入了$1{\times}1$的卷积核来减少数据流的深度,这样就降低了参数数量与运算量。
Interception Module最终会将四个运算结果沿深度轴拼接起来,那么四个运算结果的数据流深度可以不同,但是尺寸必须相同。一个Interception Module中可能的数据流尺寸如下图所示:

注意到$1{\times}1$卷积核所在层的数据流深度,比其上一层与其下一层的数据流都要小,所以$1{\times}1$卷积核所在的层也叫做“瓶颈层”(bottleneck layer)。
完整的GoogLeNet结构如下图所示:
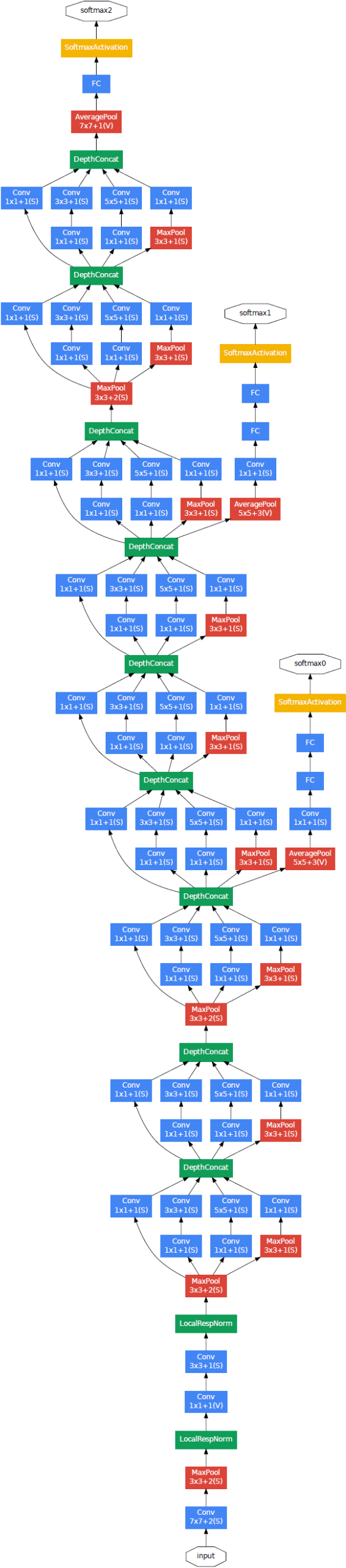
关于GoogLeNet,值得一提的有几点:
- 在最后一个Module之后有一个AveragePool层,其目的是为了替代传统的FC层,大大减少参数量,其后添加的FC层只是为了便于调优
- 在网络中间层添加了两个额外的中间输出,目的是为了避免梯度消失;同时中间输出会以一定的权重加到最终输出上去
- Interception Module背后的思想在于,不同的操作,如不同大小的卷积或池化,它们所看到的视野域是不同的,将不同大小的卷积核或池化核并行应用于特征图,可以同时看到多种信息
一个不完整的GoogLeNet实现示例见这里。
ResNet
有人经过实际测试发现,单纯的将网络加深并不能提升网络的表现,深层网络的表现反而还不如浅层网络,甚至深层网络在训练集上的误差都要高于浅层网络。这个结论是反直觉的,因为如果深层网络是容易过拟合的话,那么至少在训练集上的表现不会弱于浅层网络,可能的解释就是深层网络的模型空间太大导致太难训练。假设在深层网络的后面几层直接将输入输出,即该层什么都不做,那么就可以得到一个与浅层网络等价的深层网络。受此启发,ResNet诞生,ResNet中的残差块(residual block)如下图所示:
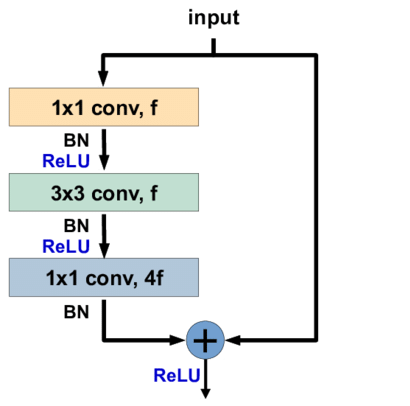
每一个残差块包含一个或两个$3{\times}3$卷积核的卷积层,除此之外,残差块在激活输出之前,会将输入加到输出上,相加时会对输入再做一次卷积保证输入输出的深度相等。之前的GoogLeNet使用了$1{\times}1$的卷积核来减少参数数量与运算量,对于过深的ResNet,同样使用瓶颈层来提高模型的训练效率。完整的ResNet结构就是若干个残差块的级联,并且ResNet的性能在深度过深时不会受到影响。原论文中给出的ResNet结构如下图所示:
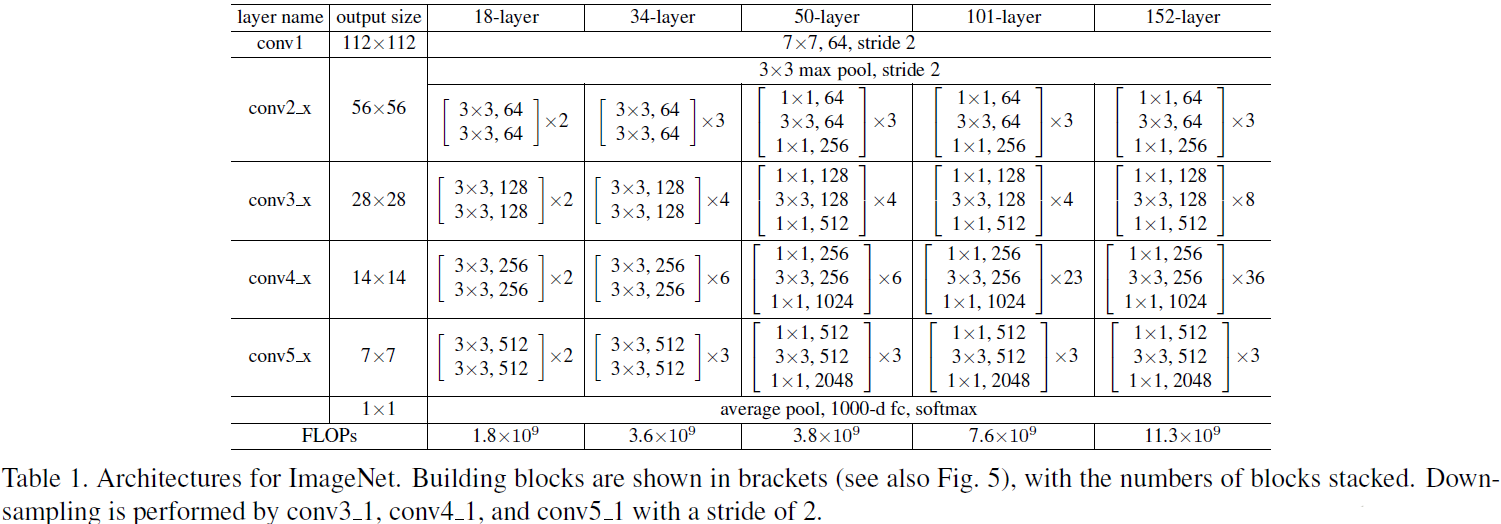
表格中方括号括起来的表示一个残差块,论文中统一将resnet中所有的残差块分为4部分:conv2、conv3、conv4和conv5,不同配置的resnet只有每个部分包含的残差块结构不同。同时还注意到类似于VGGNet,resnet中的数据流服从一个规律:数据尺寸逐渐减倍,数据流深度逐渐加倍。ResNet在最后同样没有直接连接FC层,大大减少了参数数量,并且使用了与GoogLeNet相同的平均池化。除此之外,还可以看到ResNet并没有使用传统的conv+pool的块结构,其分别在起始和结束处放置了一个最大池化与平均池化,中间层是不含池化层,也就是说ResNet仅使用卷积核去同时完成卷积与降采样的过程。
一个非完整的ResNet示例见此。
CNN相关计算
到目前为止,以上CNN架构都是在网络结构上做优化,那么现在停下来分析一下CNN中卷积操作在计算上的复杂度。首先定义几个变量,假设CNN的输入数据尺寸与中间的特征图都是正方形,那么定义输入特征图的尺寸为$(D_{I},D_{I},C_{I})$,输入特征图的尺寸为$(D_{O},D_{O},C_{O})$,卷积核的尺寸为$(D_{K},D_{K},C_{I})$,卷积核的数量为$C_{O}$。
在标准卷积操作下,每一次卷积操作的计算量为:$D_{K}^{2}\times{C_{I}}$,一个卷积核的总计算量为:$D_{K}^{2}\times{C_{I}}\times{D_{O}^{2}}$,所有卷积核的总计算量为:
\[comp=D_{K}^{2}\times{C_{I}}\times{D_{O}^{2}}\times{C_{O}}\]有论文尝试更改卷积运算,主要有以下两种方式。
Depthwise Separable Convolution

深度可分离卷积(DSC)不再对特征图的整个深度上做卷积,而是使用$C_{I}$个尺寸为$(D_{K},D_{K},1)$的卷积核分别对特征图做depthwise的卷积。不难看出DSC无法改变特征图的深度,所以这种卷积操作下有$C=C_{I}=C_{O}$。DSC的每一次卷积计算量为:$D_{K}^{2}$,一个核的总计算量为:$D_{K}^{2}\times{D_{O}^{2}}$,所有核的总计算量为$D_{K}^{2}\times{D_{O}^{2}}\times{C}$。
Pointwise Convolution
点卷积(PC)已经在之前的Googlenet与resnet中出现过了,即$1\times{1}$的卷积核,在之前的网络中用于缩小深度减少参数量。与DSC恰好相反,DSC可以改变数据流的尺寸但无法改变深度,而PC只能改变深度无法改变尺寸,所以这里有$D=D_{F}=D_{K}$。那么这里来分析一下,PC的每次卷积计算量为$C_{I}$,单个核的计算量为$C_{I}\times{D^{2}}$,总计算量为$C_{I}\times{D^{2}}\times{C_{O}}$。
MobileNet
基于对卷积操作的改进,Google提出了轻量级的CNN架构——MobileNet,其可用于移动设备。其主要思想就是结合使用DSC与PC两种卷积方式,大大降低了参数量与计算量。
在standard convolution操作下,计算量为:
\[comp_{std}=D_{K}^{2}\times{C_{I}}\times{D_{O}^{2}}\times{C_{O}}\]级联DSC+PC时的计算量为:
\[\begin{aligned} comp_{cas}&=D_{K}^{2}\times{D_{O}^{2}}\times{C_{I}}+C_{I}\times{D_{O}^{2}}\times{C_{O}} \\ &=D_{O}^{2}C_{I}(D_{K}^{2}+C_{O}) \end{aligned}\]计算量为之前的:
\[\begin{aligned} \frac{comp_{cas}}{comp_{std}}&=\frac{D_{O}^{2}C_{I}(D_{K}^{2}+C_{O})}{D_{K}^{2}\times{C_{I}}\times{D_{O}^{2}}\times{C_{O}}} \\ &=\frac{D_{K}^{2}+C_{O}}{D_{K}^{2}C_{O}} \\ &=\frac{1}{D_{K}^{2}}+\frac{1}{C_{O}} \\ \end{aligned}\]MobileNet中级联结构(DSC+PC)的具体构成如下图所示:
完整的网络结构如下表所示,其中Conv dw即级联结构。