神经网络
模型结构

上图是一个简单的神经网络,$x_{i}$为样本特征,$\hat{y}$为网络输出,个变量之间的关系满足:
\[\begin{aligned} a^{[1]}&=\sigma(\sum\limits_{i=1}^{3}\theta^{[0]}_{i}x_{i}+b^{[0]}) \\ \hat{y}&=g(\sum\limits_{i=1}^{4}\theta^{[1]}_{i}a^{[1]}+b^{[1]}) \\ \end{aligned}\]其中$\sigma(x)$称为激活函数(activation function),$g(x)$为输出激活函数;输入数据$X$所在的位置称为输出层(input layer),$a_{i}^{j}$所在的位置称为隐藏层(hidden layer),输出预测结果的称为输出层(output layer),图中每一个圆圈称为神经元(Neuron)。
最常见的激活函数为$\sigma(x)=\frac{1}{1+e^{-x}}$,即logistics regression中的sigmoid函数;而输出激活函数需要根据模型任务来定,回归任务下为$g(x)=x$,二分类任务下$g(x)=\frac{1}{1+e^{-x}}$,多分类任务下$g(x)=softmax(这里待补充)$;损失函数也由具体任务来定。
数学原理
保持与代码实现上的一致性,令
\[a^{[1]}=\sigma(x\theta^{[0]}+b^{[0]})\]$x$的形状为$(1,3)$,$a^{[0]}$的形状为$(1,4)$,那么有矩阵乘法的性质得$\theta^{[0]}$的形状为$(3,4)$;
\[\hat{y}=\sigma(a^{[1]}\theta^{[1]}+b^{[1]})\]$\hat{y}$的形状为$(1,1)$,所以$\theta^{[1]}$的形状为$(4,1)$。由矩阵乘法性质不难推出,若当前层的单元数为$n^{[i]}$,下层单元数为$n^{[i+1]}$,则当前层权重矩阵的形状为:
\[dim(\theta^{[i]})=(n^{[i]},n^{[i+1]})\]整个网络的输出可以写成:
\[\begin{aligned} z^{[1]}&=a^{[0]}\theta^{[0]}+b^{[0]} \\ a^{[1]}&=\sigma(z^{[1]}) \\ z^{[2]}&=a^{[1]}\theta^{[1]}+b^{[1]} \\ a^{[2]}&=\sigma(z^{[2]}) \\ \end{aligned}\]以二分类为例,简单写下神经网络的反向传播过程。为便于后面的计算,先明确$\sigma(x)=\frac{1}{1+e^{-x}}$的导数:
\[\begin{aligned} \frac{\partial{\sigma(x)}}{\partial{x}}&=\frac{-1}{(1+e^{-x})^{2}}\cdot(-e^{-x}) \\ &=\frac{1}{1+e^{-x}}\cdot\frac{e^{-x}+1-1}{1+e^{-x}} \\ &=\frac{1}{1+e^{-x}}\cdot(1-\frac{1}{1+e^{-x}}) \\ &=\sigma(x)\cdot(1-\sigma(x)) \\ \end{aligned}\]首先,损失函数为:
\[L=-y{\ln}a^{[2]}-(1-y){\ln}(1-a^{[2]})\]逐层对变量求导:
\[\begin{aligned} {\Delta}a^{[2]}&=\frac{\partial{L}}{\partial{a^{[2]}}} \\ &=-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}} \\ {\Delta}z^{[2]}&={\Delta}a^{[2]}\cdot\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}} \\ &={\Delta}a^{[2]}{\cdot}a^{[2]}(1-a^{[2]}) \\ &=a^{[2]}-y \\ {\Delta}\theta^{[1]}&={\Delta}z^{[2]}\cdot\frac{\partial{z^{[2]}}}{\partial\theta^{[1]}} \\ &={\Delta}z^{[2]}{\cdot}a^{[1]} \\ {\Delta}b^{[1]}&={\Delta}z^{[2]}\cdot\frac{\partial{z^{[2]}}}{\partial{b^{[1]}}} \\ &={\Delta}z^{[2]} \\ \end{aligned}\]更前一层的梯度为:
\[\begin{aligned} {\Delta}a^{[1]}&={\Delta}z^{[2]}\cdot\frac{\partial{z^{[2]}}}{\partial{a^{[1]}}} \\ &={\Delta}z^{[2]}\cdot\theta^{[1]} \\ {\Delta}z^{[1]}&={\Delta}a^{[1]}\cdot\frac{\partial{a^{[1]}}}{\partial{z^{[1]}}} \\ &={\Delta}z^{[2]}\cdot\theta^{[1]}{\cdot}a^{[1]}(1-a^{[1]}) \\ {\Delta}\theta^{[0]}&={\Delta}z^{[1]}\cdot\frac{\partial{z^{[1]}}}{\partial\theta^{[0]}} \\ &={\Delta}z^{[1]}{\cdot}a^{[0]} \\ {\Delta}b^{[0]}&={\Delta}z^{[1]}\cdot\frac{\partial{z^{[1]}}}{\partial{b^{[0]}}} \\ &={\Delta}z^{[1]} \end{aligned}\]这是使用sigmoid函数为激活函数下二分类神经网络的梯度。其实如果在更深层的神经网络中推导的话,假设有$h$层隐藏层,那么除了最后一层隐藏层,前$h-1$层的梯度都可以写成递推表达式,因为最后一层隐藏层的梯度是由损失函数推出来的,而前$h-1$层的梯度都是由当前层的输出$a$推出来的。递推式展开可以写成累乘,那么累乘就会有一个问题:当神经网络层数过深并且每一层的梯度都小于1时,那么越前面层的梯度就会越小,若都大于1,则越前面层的梯度就会越大。这就是深层神经网络中梯度消失与梯度爆炸的问题。
Activation Function
sigmoid
DNN初期默认采取的激活函数是sigmoid函数:
\[\sigma(x)=\frac{1}{1+exp(-x)}\]该函数图像为:

可以看到该函数在$\pm{5}$处就几乎达到阈值了,相对应的是一个梯度饱和问题。每一层激活函数的输入是$z^{[i]}=a^{[i-1]}\theta^{[i-1]}+b^{[i-1]}$,如果这个值稍微大一点(超出$\pm{5}$),那么就会导致该层激活函数的梯度变得及其微小,影响反向传播算法的执行。
另外,sigmoid函数的输出范围是$(0,1)$,这会带来另一个隐含问题。每一层的输出都是正的,那么该层对于优化参数的局部梯度为:$\frac{\partial{a^{[i+1]}}}{\partial{w^{[i]}}}=a^{[i+1]}(1-a^{[i+1]})a^{[i]}$,该值恒为正。在梯度下降法的优化过程中,该特性会导致参数在一次迭代中要么都往正方向更新,要么都往负方向更新,相当于每次更新参数都沿轴向更新。
sigmoid函数的第三个缺点就是其中的指数函数需要一定的计算量。
tanh
DNN激活函数的另一个选择:
\[tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\]其图像为:
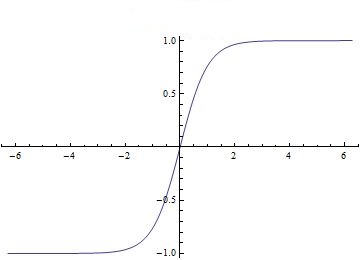
可以看到tanh函数把输入映射到了$(-1,1)$区间,虽然对梯度下降法的收敛有一定加速作用,但是对于sigmoid函数存在的另外两个问题,tanh函数同样存在,甚至比sigmoid函数更严重。
Rectified Linear Unit
整流线性单元(ReLU)激活函数的表达式为:
\[f(x)=max(0,x)\]其有如下优点:
- 在正域上不存在函数上限,也不会存在梯度饱和的问题
- 计算简单
- 收敛速度快于sigmoid激活函数
- 更符合生物神经学
不过因为ReLU的左半边恒为0,右边恒为正,同样存在一个隐含的问题。ReLU函数在计算梯度时对负值是不响应的,负域的梯度恒为$0$,如果在反向传播时传过来一个负的梯度值,那么该神经元再往前传播时的梯度贡献始终是$0$,相当于该神经元已“坏死”。在某些情况下,如果在模型的整个训练过程中,经过该神经元的梯度始终是负的,那么该神经元在整个训练过程持续性“坏死”,甚至还会影响到前面层的神经元,产生连锁反应,导致前面的神经元更容易“坏死”或“持续性坏死”。
Leaky ReLU
带泄露的ReLU是为了解决ReLU“坏死”问题而出现的,其表达式为:
\[f(x)=max(0.01x,x)\]其图像跟ReLU的区别在于负域,Leaky ReLU的负域不恒为零,而是一个稍微倾斜的直线,这样就避免了神经元“坏死”的问题。同时Leaky ReLU还有一个变种,当把负域直线的斜率参数化后,就得到了Parametric ReLU:
\[f(x)=max({\alpha}x,x)\]其中$\alpha$为$(0,1)$区间的任何值。Leaky ReLU与PReLU的缺点显而易见:引入了额外的超参数,并且在实践上不见得比ReLU好。
ELU
待补充,其优点没太看懂
Weight Initialization
Constant Initialization
如果把所有的权重参数都初始化为同样的常数,那么同一层的所有的神经元只等效为一个神经元。
Small random numbers
对于小型网络,常见的初始化方法为初始化一个服从$\mathcal N(0,0.01)$的随机分布。但是该策略对大型网络而言并不是一个好选择,考虑前向传播过程,由前往后每一层的输出会越来越小,直至为$0$,在反向传播过程中同样会造成梯度消失的问题。
类似地,如果权重初始化的太大,对于某些激活函数如sigmoid与tanh而言,会导致每一层激活后的输出都在饱和区域,该层对参数的梯度非常小,然后造成梯度消失。
Xavier Initialization
看出权重参数初始化得太大或太小都不好,对于有饱和区的激活函数而言,需要尽量避免激活输出进入饱和区。在讲Xavier之前,先回顾一下方差的一些性质,对于独立同分布的变量而言,有
\[\begin{aligned} D(X+Y)&=D(X)+D(Y) \\ D(XY)&=D(X)D(Y)+D(X)E(Y)^{2}+D(Y)E(X)^{2} \\ \end{aligned}\]若各变量都是零均值,上式可以写为:
\[\begin{aligned} D(X+Y)&=D(X)+D(Y) \\ D(XY)&=D(X)D(Y) \\ \end{aligned}\]现假设权重参数$\theta$与输入数据$x$都为零均值,方差$v$的独立同分布变量,那么在忽略偏置项时某一层的线性输出为:
\[z^{[1]}=x\theta^{[0]}=\sum\limits_{n_{I}}x_{j}\theta_{j}^{[0]}\]其中$n_{I}$表示上一层的神经元数。那么可以得到,当前层线性输出值的均值为$0$,方差为:$v_{z^{[1]}}=n_{I}{\times}v_{x}{\times}v_{\theta^{[0]}}$。我们希望的是每一层的输入与输出尽量同分布,那么令$v_{z^{[1]}}=v_{x}$,得:$v_{\theta^{[0]}}=1/n_{I}$。上面只考虑了正向传播,那么在反向传播时,同样希望每一层的参数梯度也同分布,那么有:$v_{\theta^{[0]}}=1/n_{O}$,其中$n_{O}$为当前层的神经元数。
Xavier Initialization的推荐做法是将权重参数初始化为一个均值为$0$,方差为$\frac{2}{n_{I}+n_{I}}$。
Optimization
为了统一各优化算法的描述,这里先借鉴该文中的方法定义一个优化算法框架。令参数为$\theta$,学习率为$\eta$,目标函数为$J$,优化过程可分为三步:
- 计算目标函数$J$关于参数$\theta$的梯度:$g=\nabla_{\theta}J$;
- 更新一阶动量$m=\phi(g)$与二阶动量$v=\psi(g)$;
- 更新参数$\theta:=\theta-\eta\frac{m}{v}$。
GD
梯度下降(gradient decent)是最经典的优化方法了,其中没有动量的概念,所以$m=g$与二阶动量$v1$,参数更新式为:
\[\theta:=\theta-\eta\cdot{g}\]梯度下降有两个变种,批量梯度下降(mini-batch GD)与随机梯度下降(Stochastic GD)。前者每次使用一个batch的数据去计算梯度更新参数,后者每次使用单个样本计算梯度更新参数。
SGD with Momentum
GD的缺点在于其学习率(步长)是固定的,Momentum的思想就是加入一个一阶动量来使得学习率会依据历史值而变化。Momentum优化方法的计算公式如下(注:这里是用的是TensorFlow中Momentum的实现方式):
\[\begin{aligned} m:=\gamma{m}+g \\ \theta:=\theta-\eta\cdot{m} \\ \end{aligned}\]可以看出Momentum一阶动量实际上是梯度的历史加权和。
待补充。
Batch Normalization
在权重参数初始化一节中讲到,如果希望神经网络学到东西,那么在正向传播时激活输出不能进入饱和区,即不能让反向传播过程中参数梯度过小,令每一层的输出与输入服从同分布即可解决该问题。Batch Normalization的思想就是预设一个分布函数,并对每一层的线性输出做操作,使其强行服从该分布。
以标准正态分布为例,BN在对每一层的线性输出都做一次Normalization,使得每层的激活函数总是接受一个服从标准正态分布的输入值:
\[\begin{aligned} z^{[i]}&=a^{[i-1]}\theta^{[i-1]} \\ \hat{z}^{[i]}&=\frac{z^{[i]}-E(z^{[i]})}{\sqrt{D(z^{[i]})}} \\ \end{aligned}\]经上述转化过后的线性输出服从标准正态分布。当然标准正态分布的线性输出只是预设的一种特殊情况,为了增强灵活性,BN在上述过程后还有一步线性变换的操作:
\[\hat{z}^{[i]}=\gamma\hat{z}^{[i]}+\beta\]最后这一部相当于把标准正态分布推广到了任意参数的正态分布,其中$\gamma$与$\beta$可以通过学习得到。不难发现,若$\gamma=\sqrt{D(z^{[i]})}$且$\beta=E(z^{[i]})$,则$\hat{z}^{[i]}=z^{[i]}$。