模型评估与选择
Bias
偏差为模型对于观测数据的拟合程度,可以理解为射箭时的准心与靶心的偏差。
Variance
方差能表征模型的稳定程度,可以理解多次射箭时各准心的分散程度。
Model Complexity
一般来说,越简单的模型具有偏差高方差低的特点,而复杂模型则恰好相反。
假设有训练集$\tau$以及模型的评估方法$L(Y,\hat{f}(X))$,那么模型的泛化误差(generalization error)可表示为:
\[Err=E[L(Y,\hat{f}(X)|\tau)]\]给定训练集下训练得到的模型$\hat{f}(X)$在整个群体$X$上的期望误差,除此之外,在训练集上还可以得到一个训练误差(training error):
\[Err_{\tau}=\frac{1}{N}L(Y_{\tau},\hat{f}(X_{\tau}))\]可惜因为variance的存在,训练误差并不能很好地作为泛化误差的估计。虽然更复杂的模型能够捕获到数据中更深层次的结构(同时也需要更多的数据),但会有过拟合的风险,就像做阅读理解的时候过度解读了一样。所以,对模型的有效评估很重要。
在数据充足的情况下,办法很简单,将已有数据进行划分,一部分作为训练集(training set)用于训练模型,另一部分用作验证集(validation set)用于检验模型在未知数据上的泛化性能。不过怎么划分数据并没有一个统一准则,一般来讲,原有数据的信噪比越大,训练集的比例可以降低;模型越简单,训练集的比例也可以降低。
偏差-方差分解
对于真实分布$Y=f(X)+\epsilon$,其中$\epsilon\sim N(0,\sigma^{2})$,那么一个模型$\hat{f}(x)$在某个样本上的期望误差为:
\[\begin{aligned} Err(x_{0})&=E[(Y-\hat{f}(x_{0}))^{2}|X=x_{0}] \\ &=\sigma^{2}+[E(\hat{f})-f]^{2}+E[\hat{f}-E(\hat{f})]^{2} \\ &=\sigma^{2}+Bias^{2}+Variance \\ \end{aligned}\]此处有上式的推导,个人没看懂,如果有懂的请指导一下,谢谢。
下面的图诠释了偏差与方差的问题:
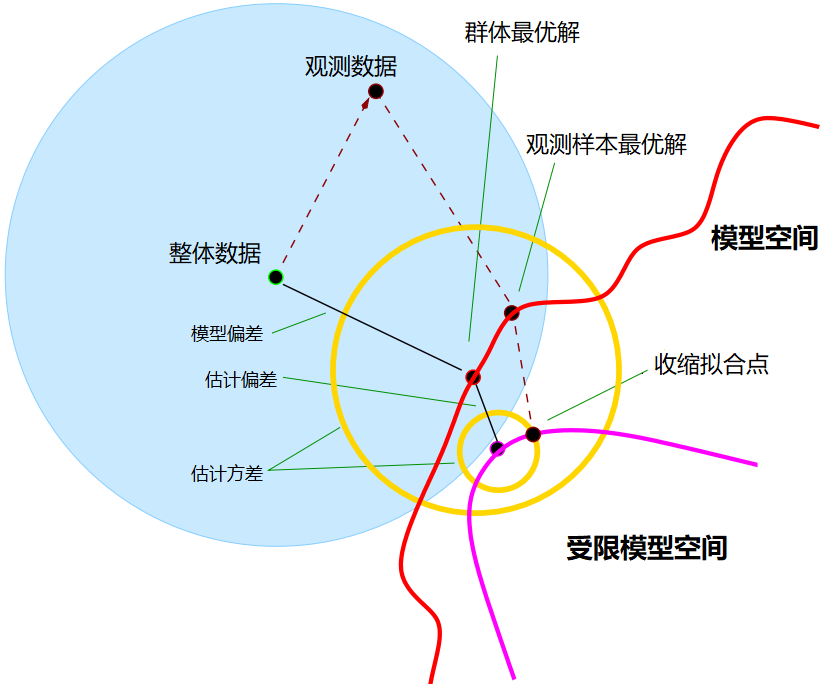
上图的蓝色范围表示的是数据真实分布;红色范围表示的是模型空间,紫色范围表示受限模型空间,模型空间由模型的拟合能力决定,模型越复杂拟合空间就越大,如神经网络理论上能拟合任意形状的函数。在选定一个特定的模型后,该模型理论上能达到的最优解为群体最优解(closest fit in population),但是由于观测样本与整体分布之间的不一致,,模型只能在已有的观测数据上进行拟合,这样的到的最优解叫做观测最优解(closest fit in realization)。某一个模型的群体最优解与真实数据分布之间的误差叫做模型偏差(model bias),这是由模型决定的,想要减小模型偏差只能换模型。另一方面,原有模型空间的复杂度与模型预测的波动性会因模型本身而改变,如图中黄色空间所示;在之前的文章中提到,一般会使用一定的误差增加来换取更高的稳定性,这就是图中的紫色空间。在受限模型空间内的最优解与原有模型空间内的最优解的距离就叫做估计偏差(estimation bias),这跟之前说的正则化等同于偏差换方差是一致的。
交叉验证
为了实现对测试误差的有效估计,最常用的方法就是做交叉验证(cross validation)。交叉验证的思想很简单,将已有数据划分成$K$份,每次将其中的一份作为验证集(validation set),而用剩下的$K-1$份数据作为训练集训练得到模型,这样就可以重复训练$K$次,可以得到$K$个验证误差(validation error),将其平均作为对测试误差的估计。
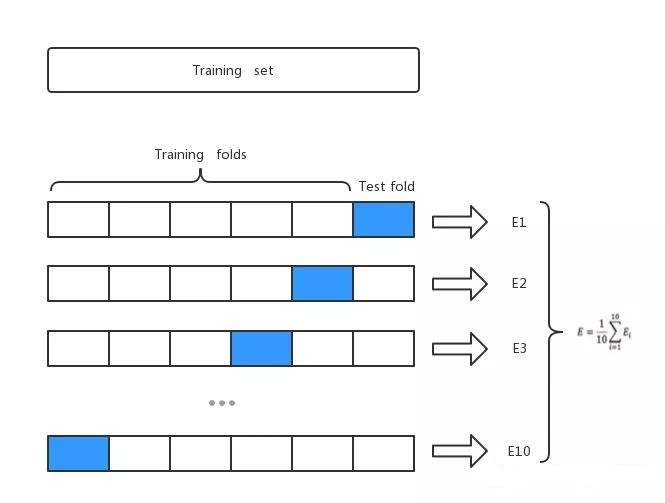
$K$的取值通常为5或10,特别的,当$K=N$时叫做留一验证法(leave-one-out)。值得一提的是,当$K$越大,验证误差与测试误差之间的偏差就越小,但是方差越大,反之亦然。
Bootstrap
Bootstrap是指有放回的抽样,假设现在有观测数据$Z=(z_{1},z_{2},…,z_{N})$,进行$B$轮有放回的抽样会得到$B$个有重叠的子样本$Z_{1},Z_{2},…,Z_{B}$。有了这些数据子集之后就可以根据这些子集来估计原本观测数据的任意统计变量,如利用bootstrap来估计整体的方差:
\[\hat{S}(Z)=\frac{1}{B-1}\sum\limits_{i=1}^{B}(S(Z_{i})-\bar{S})^{2}\]其中$\bar{S}=\frac{1}{B}\sum\limits_{i=1}^{B}S(Z_{i})$,为使用子样本对整体的均值估计。
现在每一轮bootstrap都是对已有数据做等体量的采样,即对有$N$个样本的数据集,每一轮bootstrap采出$N$个样本作为数据子集,那么容易得到,每一个样本被采到的概率为:
\[\begin{aligned} P(IN)&=1-P(NOT \ IN)^{N} \\ &=1-(1-\frac{1}{N})^{N} \\ &=1-\frac{1}{e} \\ &=0.632 \end{aligned}\]由此可以看出,每一轮bootstrap得到的样本子集$Z_{i}$大概只包含了原观测数据的63.2%,因此原数据中未被抽到的36.8%可以用作模型验证,前面的文章也提到过,这叫包外误差估计。但是包外误差估计有一个问题,就是在验证模型中只用了大约2/3的数据去训练模型,这样得出的误差估计值差不多相当于使用3折交叉验证或2折交叉验证。如果该模型关于该数据的学习曲线在$\frac{N}{2}$到$\frac{2N}{3}$区间有很明显的提升的话,那么包外误差估计得到的验证效果只是测试误差的一个悲观估计(Pessimistic estimate)。
为了提升包外估计的准确性,引入训练误差,并赋以权重,得到改进的.632估计:
\[\hat{Err}^{.632}=0.368{\times}Err_{train}+0.632{\times}Err_{validation}\].632估计在过拟合的情况下表现会很糟糕。比如现在有一个二分类问题,模型在训练集上过拟合导致$Err_{train}=0$,而在验证集上表现我们取一个最低值$0.5$,那么.632估计给出的验证误差为:
\[\begin{aligned} \hat{Err}^{.632}&=0.368{\times}0+0.632{\times}0.5 \\ &=0.316 \end{aligned}\]可以看到,.632估计在过拟合的情况下会给出一个乐观估计。
.632+估计,待补充。