模型概述
假定有一组数据$X$与$Y$,其中
\[X= \left[ \begin{matrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(m)} \\ \end{matrix} \right]\]$X$总共包含$m$条数据,而每条数据$x^{(i)}$又可表示为:
\[x^{(i)}= \left[ \begin{matrix} x^{i}_{1} & x^{i}_{2} & \cdots & x^{i}_{n} \end{matrix} \right]\]$Y$是一组向量,具体展开为:
\[Y= \left[ \begin{matrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \\ \end{matrix} \right]\]$y^{i}$为连续型数值,如果需要使用$x^{i}$的值来拟合$y^{i}$,最简单的模型就是如下形式的线性模型:
\[\begin{aligned} \hat{y}^{(i)} &= \theta_{0}+\theta_{1}x^{(i)}_{1}+...+\theta_{n}x^{(i)}_{n} \\ &= x^{(i)}\theta^{T} \\ \end{aligned}\]当我们使用一个线性模型去拟合数据时,我们就默认假定了$y^{i}$是服从线性分布的,再引入一个随机误差项,可得真实数据值得表达式为:
\[y^{(i)}=f(x^{(i)})+\epsilon^{(i)}\]$\epsilon$是一个完全随机噪声,与数据中的$X$与$Y$都没有关系,也被叫做不可规约误差(irreducible error)。我们的任务就是使用$\hat{f}(x)=X\theta^{T}$去拟合$f(x)$,$\hat{f}(x)$与$f(x)$之间的误差称为可规约误差(reducible error)。
再假设噪声$\epsilon^{(i)}$服从正态分布$\epsilon \sim N(0, \sigma^{2})$,那么在完美拟合的条件下,有$y^{(i)} \sim N(x^{(i)}\theta^{T},\sigma^{2})$:
\[p(y^{i}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\hat{y}^{(i)})^{2}}{2\sigma^{2}})\]那么,对于参数$\theta$的似然函数为:
\[\begin{aligned} L(\theta) &= \prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta) \\ &= \prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\hat{y}^{(i)})^{2}}{2\sigma^{2}}) \\ \end{aligned}\]其对数似然函数为:
\[\begin{aligned} l(\theta) &= \ln{L(\theta)}\\ &= \sum_{i=1}^m [\ln{\frac{1}{\sqrt{2\pi}\sigma}}-\frac{(y^{(i)}-\hat{y}^{(i)})^{2}}{2\sigma^{2}}] \\ &= m\ln{\frac{1}{\sqrt{2\pi}\sigma}}-\frac{1}{2\sigma^{2}}\sum_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^{2} \end{aligned}\]最大化似然函数等价于最小化下面的式子:
\[J(\theta)=\frac{1}{2}\sum_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^{2}\]一些前提假设
- 各特征之间相互独立
现在以二元情况为例,再仔细看一下linear regression模型的表达式:
\[\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}\]注意,在这里其实还有一个隐藏的前提假设,即$x_{1}$与$x_{2}$无关(相互独立)。如果在某一情景下,这两个特征之间本来就存在着关系,如$x_{2}=f(x_{1})$这样的关系,那么上述模型的表达式就不准确。那么准确的linear regression模型表达式应为:
\[\begin{aligned} \hat{y}&=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}(x_{1}x_{2}) \\ &=\theta_{0}+\theta_{1}x_{1}+(\theta_{2}+\theta_{3}x_{1})x_{2} \end{aligned}\]其中,$x_{1}x_{2}$称为交互项,代表的是一个线性关系。
- 原特征与目标变量服从一元线性关系
可以加入已有特征的高次项使得模型能够捕获非线性关系,如:
\[\begin{aligned} \hat{y}&=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{1}^{2} \\ &=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}^{2} \end{aligned}\]这叫做polynomial regression,本质上还是一个linear regression。
- 误差项之间相互独立
一般来说会认为各样本之间的预测误差$\epsilon_{i}$与$\epsilon_{j}$之间是没有关联的,但是在时序数据中,相邻时间点的样本误差可能会存在联系。
如下图是一幅残差与时序的关系图,可以看到残差的分布与时间并无关系,模型的残差是随机分布的:
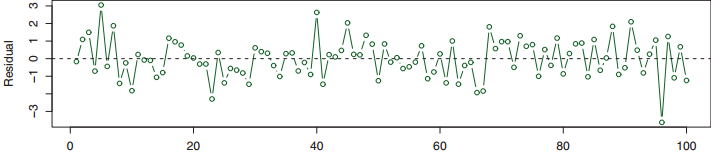
但是再看下图,残差与时间的关系中具有一定的模式,相邻时间点的样本残差很相似,就说明残差之间是有关系的:

- 误差项的方差为常数
在建立线性模型时,假设了真实数据中的噪声分布是服从正态分布\(\epsilon \sim N(0, \sigma^{2})\)的,分布的方差为一常数\(\sigma^{2}\)。但在实际中,预测值与真实值之间的误差分布方差不是一个常数,而是会随着\(Y\)的增大而增大,从直观上来说就是目标值越大则越难预测准,此时的残差与\(Y\)的关系如下图所示:
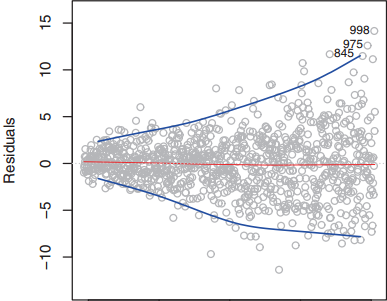
那么,为了抑制误差项的方差,解决的方法也很简单,想办法抑制目标变量$Y$的取值范围即可,可以通过凹函数变换,如$\sqrt{Y}$或$\log(Y)$来处理目标变量。
- 理想数据集无异常值
在真实数据集中,会因为各种原因而引入异常数据,而异常数据又会影响模型对已有数据的拟合。那么可以通过绘制studentized residual与$Y$的关系图来判断异常数据点。其中studentized residual的计算方式为$\frac{\epsilon_{i}}{\sigma}$,该指标实际上就是用于检测各样本的残差是否符合正态分布,若某样本的studentized residual不在$[-3,3]$区间内,则基本可以断定该样本点为异常点。
- 每个样本点对模型参数的贡献是均匀的
之前的叙述都是假设模型的参数$\theta$是由所有样本点共同产生贡献而得出的,并且每个样本点对参数所作的贡献也相差无几。如果数据集中存在某几个点,能够对模型的最终参数产生很大的影响甚至是决定性影响,那么这些样本点就叫做杠杆支点(high leverage points)。
优化策略
梯度下降法
我们对需要优化的参数\(\theta\)进行随机初始化,然后我们使用每次向着最优解行进一小步的策略来实现多次迭代找到最优解。这里用到的原理就是梯度的概念,目标函数对于参数的梯度实际上就是指向极值的方向,于是使用下面公式来更新参数$\theta$:
\[\theta:=\theta-\alpha\nabla_{\theta}{J(\theta)}\]均方误差公式的求导太过简单,这里不再写出。
梯队下降法的优劣
梯度下降法的优点在于:
- 计算简单
- 参数更新的方向始终是朝着最优解或次优解
缺点是:
- 如果目标函数是非凸的,算法可能陷入一个局部最优解
- 每次计算梯度都必须使用整个训练数据集,空间开销大
梯度下降法还存在几个变种,分别是:
- 分批梯度下降:每次计算梯度只使用一小批数据
- 随机梯度下降:每次计算梯度只使用一条数据
这两个变种都能适当弥补原始梯度下降法的缺陷。
正规方程
线性回归的方程可写为:
\[\hat{Y}=X\theta^{T}\]损失函数为:
\[\begin{aligned} MSE&=\sum_{i=1}^{m}(y^{(i)}-x^{(i)}\theta^{T})^{2} \\ &=(Y-X\theta^{T})^{T}(Y-X\theta^{T}) \end{aligned}\]损失函数对参数$\theta$求导并令其为零,得:
\[X^{T}(Y-X\theta^{T})=0 \\ X^{T}Y=X^{T}X\theta\]如果$X^{T}X$是非奇异矩阵,那么最佳参数$\theta$为:
\[\hat{\theta}=(X^{T}X)^{-1}X^{T}Y\]引入先验分布的参数模型(正则化)
到目前为止,上面所讲述的线性模型,我们只对数据中的噪声做了一个先验假设$\epsilon \sim N(0, \sigma^{2})$,那么求出来的解一定是对已有数据(观测值)的一个最优解。但是,对已有数据的最优解不一定对未知数据也是最优解,那么还需要对隐藏的真实分布$Y=X\theta^{T}$中的参数$\theta$再做一个先验假设。
Laplace distribution
令$\theta \sim Laplace(0,\beta)$,那么依照前文,参数$\theta$的似然函数为:
\[\begin{aligned} L(\theta) &= \prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)\prod_{j=1}^mp(\theta_{j}) \\ &= \prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\hat{y}^{(i)})^{2}}{2\sigma^{2}})\prod_{j=1}^m\frac{1}{2\beta}exp(-\frac{|\theta_{j}|}{\beta}) \\ &=\frac{1}{(\sqrt{2\pi}\sigma)^{m}}exp(-\frac{1}{2\sigma^{2}}\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2})\cdot\frac{1}{(2\beta)^{m}}exp(-\frac{1}\beta\sum_{j=1}^{m}|\theta_{j}|) \\ \end{aligned}\]对数似然函数为:
\[\begin{aligned} \ln L(\theta) &= m\ln\frac{1}{\sqrt{2\pi}\sigma^{2}}+m\ln\frac{1}{2\beta}-\frac{1}{2\sigma^{2}}\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2}-\frac{1}{\beta}\sum_{j=1}^{m}|\theta_{j}|) \\ \end{aligned}\]最大化上式等价于最小化下式:
\[J(\theta,\lambda)=\frac{1}{2}\sum_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^{2}+\lambda||\theta||_{1}\]此为带L1正则的线性回归,也称LASSO。
Gaussian distribution
令$\theta \sim N(0,\beta^{2})$,那么依照前文,参数$\theta$的似然函数为:
\[\begin{aligned} L(\theta) &= \prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)\prod_{j=1}^mp(\theta_{j}) \\ &= \prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\hat{y}^{(i)})^{2}}{2\sigma^{2}})\prod_{j=1}^m\frac{1}{\sqrt{2\pi}\beta}exp(-\frac{\theta_{j}^{2}}{2\beta^{2}}) \\ &=\frac{1}{(\sqrt{2\pi}\sigma)^{m}}exp(-\frac{1}{2\sigma^{2}}\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2})\cdot\frac{1}{(\sqrt{2\pi}\beta)^{m}}exp(-\frac{1}{2\beta^{2}}\sum_{j=1}^{m}\theta_{j}^{2}) \\ \end{aligned}\]对数似然函数为:
\[\begin{aligned} \ln L(\theta) &= m\ln\frac{1}{\sqrt{2\pi}\sigma^{2}}+n\ln\frac{1}{\sqrt{2\pi}\beta^{2}}-\frac{1}{2\sigma^{2}}\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2}-\frac{1}{2\beta^{2}}\sum_{j=1}^{m}\theta_{j}^{2}) \\ \end{aligned}\]最大化上式等价于最小化下式:
\[J(\theta,\lambda)=\frac{1}{2}\sum_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^{2}+\lambda||\theta||_{2}\]此为带L2正则的线性回归,也称Ridge Regression。
通用正则化
考虑了L1与L2正则化后,不难推出正则化还有一种通用形式:
\[J(\theta,\lambda)=\frac{1}{2}\sum\limits_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2}+\lambda\sum\limits_{j=1}^{m}\theta_{j}^{p}\]对于不同的$p$值,其边界条件如下图所示:
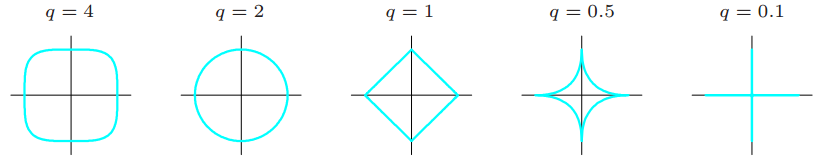
不过实践证明,去尝试除了$(0,1,2)$之外的$p$值并不值得,反而将$p$值限定在$(1,2)$之间能达到一个Ridge与Lasso的折中。不过还有一种方法就是同时结合Ridge与Lasso,形成一个ElasticNet正则项:
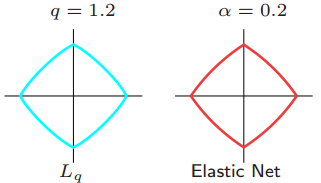
\[J(\theta,\lambda)=\frac{1}{2}\sum\limits_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^{2}+\lambda\sum\limits_{j=1}^{m}[\alpha\theta_{j}^{2}+(1-\alpha)|\theta_{j}|]\]下图是一个$L_{1.2}$与ElasticNet的边界对比:
正则化的另一个好处
上面已经讲过,数据中的各变量可能是有相互关系的,除了引入交互项捕捉这种关系之外,还可以做特征选择。对于有$n$个特征的数据,可以尝试所有可能的组合数来找到一个最佳特征子集。不过暴力搜索的代价太高,可以以RME为指导来做特征选择;另一方面,模型关于原数据集的最优解$\hat{\theta}$在未知数据上不一定是最优解,选出一部分特征也有助于提升模型的泛化性。
考虑选出一个特征子集,模型可以用下式来描述:
\[\hat{\theta}=arg\ min \sum_{i=1}^{m}(y^{(i)}-\sum_{j=1}^{n}\theta_{j}x_{ij})^{2} \qquad s.t.\sum_{j=1}^{n}I(\theta_{j}\ne0)\le{s}\]其中$I(x)$是一个指示函数,$s$是事先设定好的特征子集大小。但是上式不好计算,因为约束条件是个非连续值,退而求其次,将约束条件转化为近似但便于计算的约束条件,有:
\[\begin{aligned} \hat{\theta}&=arg\ min \sum_{i=1}^{m}(y^{(i)}-\sum_{j=1}^{n}\theta_{j}x_{ij})^{2} \qquad s.t.\sum_{j=1}^{n}|\theta_{j}|\le{s} \\ \hat{\theta}&=arg\ min \sum_{i=1}^{m}(y^{(i)}-\sum_{j=1}^{n}\theta_{j}x_{ij})^{2} \qquad s.t.\sqrt{\sum_{j=1}^{n}\theta_{j}^{2}}\le{s} \\ \end{aligned}\]转化后的约束条件是可计算的,下面详细讨论一下这几种约束。
注意到,以上三种约束分别等同于三种范数:
\[\begin{aligned} \sum_{j=1}^{n}I(\theta_{j}\ne0)&=||\theta||_{0} \\ \sum_{j=1}^{n}|\theta_{j}|&=||\theta||_{1} \\ \sqrt{\sum_{j=1}^{n}\theta_{j}^{2}}&=||\theta||_{2} \\ \end{aligned}\]分别对应L0、L1、L2正则化,这三种正则化分别被称作Subset、Lasso和Ridge,表达式为:
\[\begin{aligned} &Subset: \qquad \hat{\theta}=arg\ min(\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})+\lambda\sum_{i=1}^{n}I(\theta_{j}\ne0)) \\ &Lasso: \qquad \hat{\theta}=arg\ min(\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})+\lambda\sum_{i=1}^{n}|\theta_{j}|) \\ &Ridge: \qquad \hat{\theta}=arg\ min(\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})+\lambda\sqrt{\sum_{i=1}^{n}\theta_{j}^{2}}) \\ \end{aligned}\]其约束范围与原问题的等值线如下图所示:
不难发现,Lasso容易导致部分特征的系数变为0,而Ridge则不会,所以,Lasso对于Ridge有一个最大的优点就是会产生解释性更强的模型。但是在预测准确率上,两者没有绝对的优劣。不过通常来说,当数据中只有一部分特征跟目标值相关时,Lasso优于Ridge;当所有特征都与目标值相关时,Ridge优于Lasso。
正则化的必要性:
- 最小二乘法虽然有高准确率、低偏差的优点,但是其方差大,通过收缩或设置某些系数为零,增加适当的偏差来降低模型的方差,能有效提升模型的泛化性
- 通过减小或者置零某些predictor的系数,可以得到解释性更强的模型
Factorization Machine
上文说到线性回归模型的一个基本假设是各特征互相独立,若考虑各个特征两两之间的相互关系,则有:
\[\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x_{1}x_{2}\]更通用的表达式为:
\[\hat{y}=\theta_{0}^{0}+\sum_{i=1}^{m}\theta_{i}^{1}x_{i}+\sum_{i=1}^{m}\sum_{j=1}^{m}\theta_{ij}^{2}x_{i}x_{j}\]其中$\theta_{\cdot}^{i}$表示第$i$阶的参数,$\theta_{\cdot}^{0}$为标量,$\theta_{\cdot}^{1}$为$(1,m)$的向量,$\theta_{\cdot}^{2}$为$(m,m)$的矩阵。
引入矩阵分解的思想,$\theta_{\cdot}^{2}=VV^{T}$,其中$V$为$(m,k)$的矩阵,则上式可以写成:
\[\hat{y}=\theta_{0}+\sum_{i=1}^{m}\theta_{i}x_{i}+\sum_{i=1}^{m}\sum_{j=1}^{m}<v_{i},v_{j}>x_{i}x_{j}\]这即是Factorization Machine的表达式。

