算法概述
K-Means算法是一种无监督分类算法,假设有无标签数据集:
\[X= \left[ \begin{matrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(m)} \\ \end{matrix} \right]\]该算法的任务是将数据集聚类成\(k\)个簇\(C={C_{1},C_{2},...,C_{k}}\),最小化损失函数为:
\[E=\sum_{i=1}^{k}\sum_{x\in{C_{i}}}||x-\mu_{i}||^{2}\]其中\(\mu_{i}\)为簇\(C_{i}\)的中心点:
\[\mu_{i}=\frac{1}{|C_{i}|}\sum_{x\in{C{i}}}x\]要找到以上问题的最优解需要遍历所有可能的簇划分,K-Mmeans算法使用贪心策略求得一个近似解,具体步骤如下:
- 在样本中随机选取$k$个样本点充当各个簇的中心点${\mu_{1},\mu_{2},…,\mu_{k}}$
- 计算所有样本点与各个簇中心之间的距离$dist(x^{(i)},\mu_{j})$,然后把样本点划入最近的簇中$x^{(i)}\in{\mu_{nearest}}$
- 根据簇中已有的样本点,重新计算簇中心 \(\mu_{i}:=\frac{1}{|C_{i}|}\sum_{x\in{C{i}}}x\)
- 重复2、3
改进
K-means算法得到的聚类结果严重依赖与初始簇中心的选择,如果初始簇中心选择不好,就会陷入局部最优解,如下图:
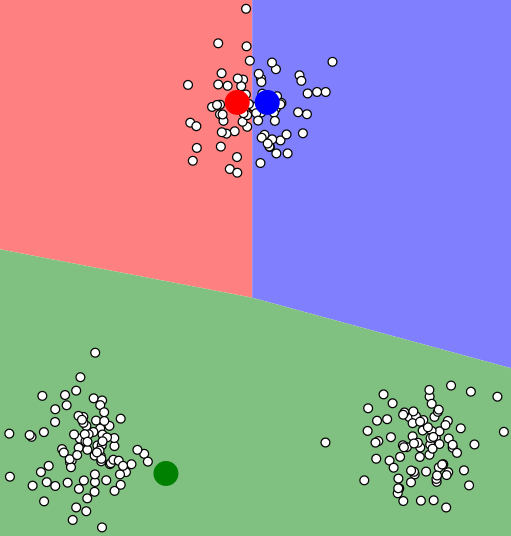
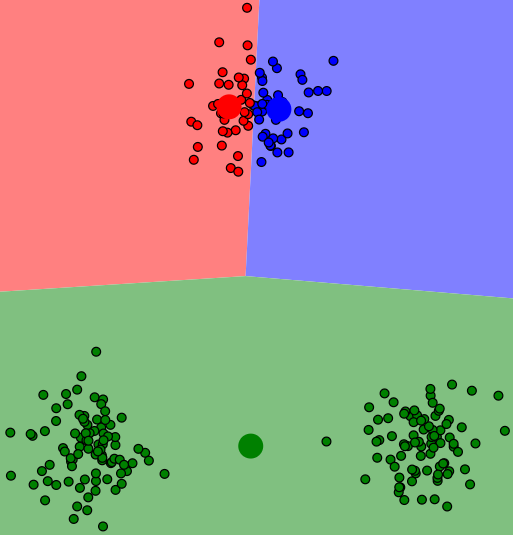
避免这种情况的简单方法是重复多次运行K-means算法,然后取一个平均结果。
另一种更精妙的方法是K-means++,它改进了K-means算法初始中心点的选取,改进后的选取流程如下:
- 在数据集中随机选取一个样本点作为第一个簇中心$C_{1}$
- 计算剩余样本点与所有簇中心的最短距离,令为$D(x^{(i)})=min[dist(x^{(i)},C_{1}),dist(x^{(i)},C_{2}),…,dist(x^{(i)},C_{n})]$,某样本点被选为下一个簇中心的概率为$\frac{D(x^{(i)})^{2}}{\sum{D(x^{(j)})^{2}}}$
- 重复2直到选出$k$个簇中心
可以看出K-means++算法的思想很简单明了,初始簇中心之间的距离应该越大越好。
标签数据
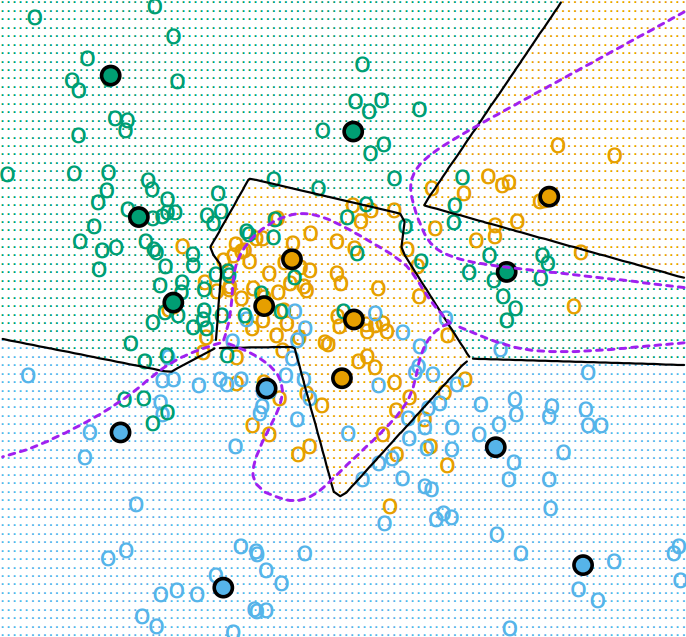
K-means算法还可用于带标签的数据,在这种情况下,K-means会对每一个类别做单独的聚类。如某数据集可分为$C$个类别,那么K-means算法会将每一个类别看做是一个单独的数据集进行聚类操作。但是在不同类的数据有重叠的情况下,类内的聚类簇也会出现重叠现象,这是因为不同类之间的内部聚类是完全独立的,这样就造成类边界处的点极易被误分。下图就是对有三个类别(绿、黄、蓝)的数据做5-means聚类,黑圆点表示的是类内簇中心,紫色虚线表示的是贝叶斯分类边界。
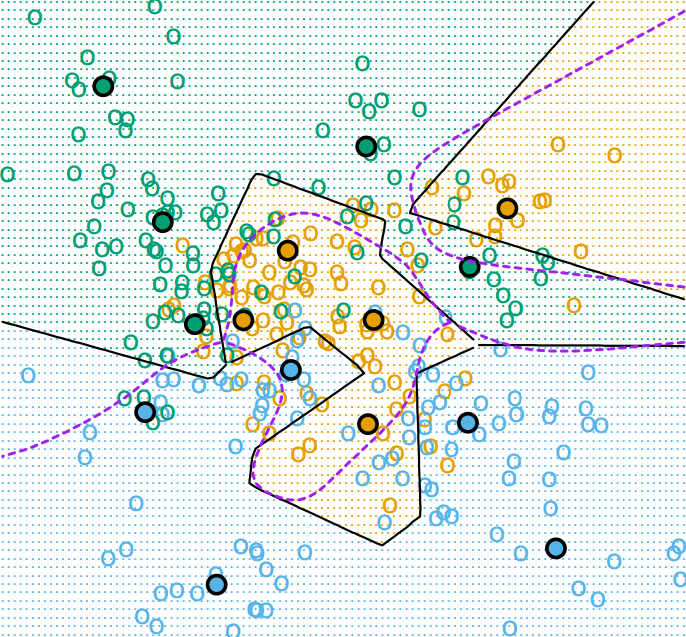
为了改进K-means在有标签数据及上的表现,有一种算法叫学习矢量量化(Learning Vector Quantization)能够利用标签信息来辅助聚类。核心思想是同类别的样本点会吸引簇中心,而不同类别的样本点会排斥簇中心,具体算法如下所示:
- 在每一个类别中都随机选取$R$个簇中心:$C_{1}^{[k]}$, $C_{2}^{[k]}$, $…$, $C_{R}^{[k]}$,$k=1, 2, …, K$
- 在所有数据中有放回地随机选取一个样本点$x_{i}$,在所有簇中心中计算找出与$x_{i}$最近的簇中心$C_{r}^{[k]}$,按照如下规则来移动簇中心$C_{r}^{[k]}$:
- 如果$C_{r}^{[k]}$与$x_{i}$同类,则将$C_{r}^{[k]}$往$x_{i}$的方向移动:$C_{r}^{[k]}:=C_{r}^{[k]}+{\alpha}(x_{i}-C_{r}^{[k]})$
- 如果$C_{r}^{[k]}$与$x_{i}$异类,则将$C_{r}^{[k]}$往$x_{i}$的反方向移动:$C_{r}^{[k]}:=C_{r}^{[k]}-{\alpha}(x_{i}-C_{r}^{[k]})$
- 重复2直到各簇中心不再变化或满足某种条件
LVQ算法中的$\alpha$为学习率,它会随着迭代次数而衰减至0。在同样的数据上应用LVQ的聚类结果如下: