概述
复习笔记,应付秋招。
Bloom filter
布隆过滤器(Bloom filter)是一种查找型数据结构,其底层原理使用了哈希映射与位操作,用于判断某一个元素是否在一个集合中。其原理如下图所示(图源wiki):
布隆过滤器使用了一个$m$位的位图用于存储已有元素的信息,而元素与位图之间的映射是通过$k$和哈希函数实现的。图中$m=18$,$k=3$,其中${x,y,z}$是已有集合,$w$是测试元素。${x,y,z}$中的每一个元素经过$3$个哈希函数映射到位图的$3$个位置并把相应的位置置$1$。在判断测试元素$w$时同样经过$3$个哈希函数得到三个对应的位置,当$3$个位置都为$1$时返回$True$。
不难看出,布隆过滤器是存在假正例(False Positive)的,即元素不在集合中却给出在集合中的结果,这是因为已存在元素可能会恰好将测试元素所对应的位置置$1$;不过布隆过滤器不存在假反例(False Negative),因为在集合中的的元素的位置是必定被置$1$的。
AVL Tree
AVL树属于二叉查找树(Binary Search Tree)的一种,其特点是能够自平衡,底层原理就在于AVL树能够通过旋转来调节自身的高度配置。首先看一下最简单的两种情况:
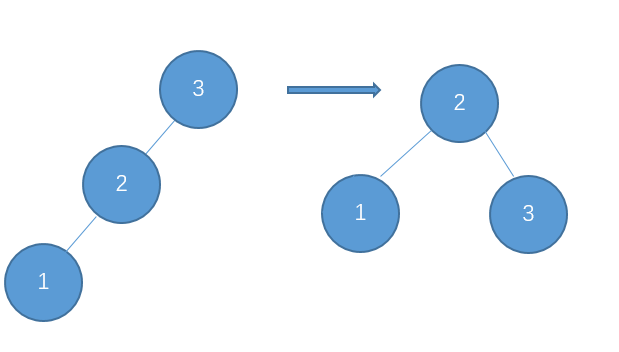
如上图这种单边不平衡的情况,旋转的方法很简单,直接将不平衡部分的中点作为新的根节点即可。另外还有一种非单边的简单情形,需要做两次旋转:
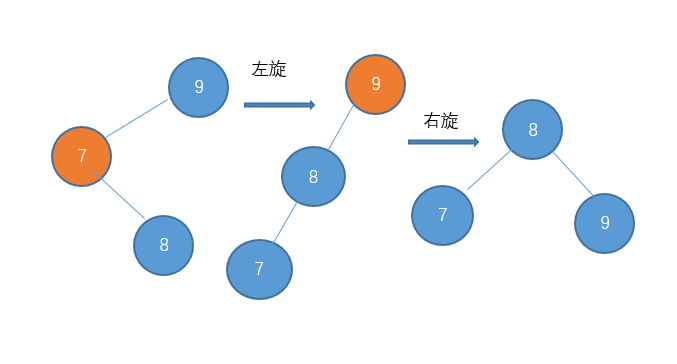
最后还有一种带子树的不平衡情形:
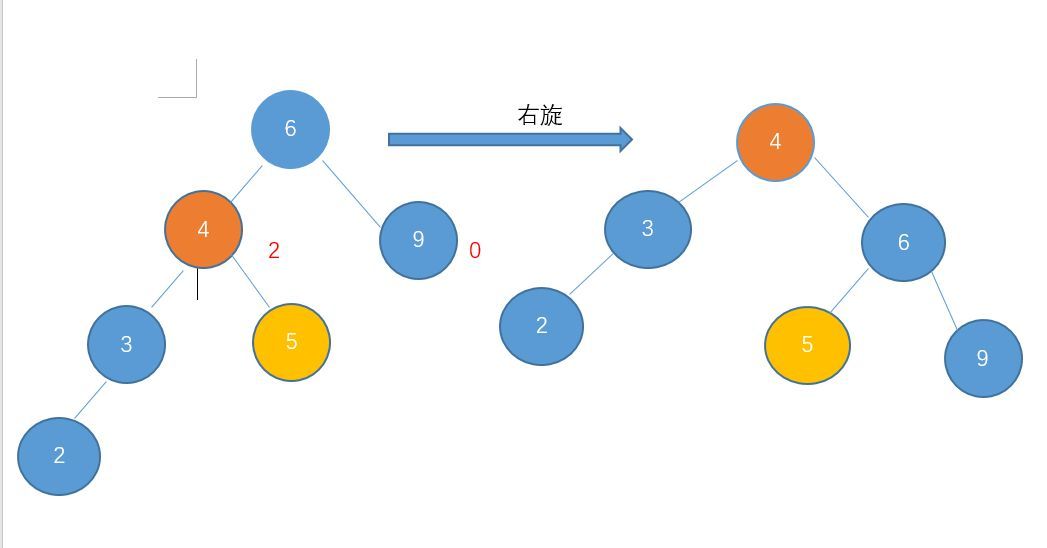
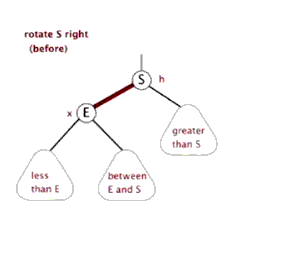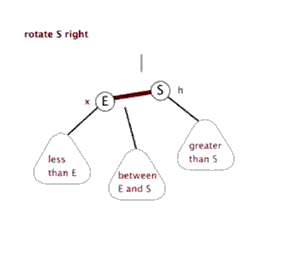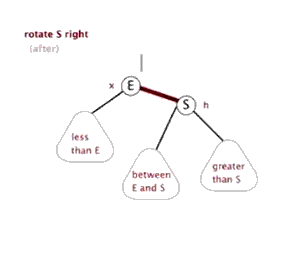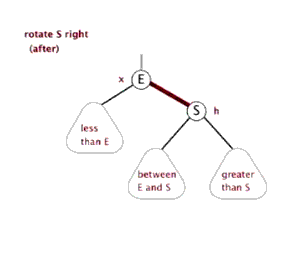
因为AVL树保证了树的平衡性,所以AVL树的查找复杂度保证为$O(\log{n})$;而插入跟删除可能会破坏树的平衡性,所以最坏情况下时间复杂度为$O(\log{n})$。
Splay Tree
伸展树(Splay Tree)同样属于BST的一种,其背后的思想是:经常被检索的元素应该放在根节点,反之放在叶节点。在伸展树中的每一次查找操作,都可能引起树的重构,最坏情况下会退化单链表。即Splay Tree最坏的查找复杂度为$O(n)$,但是其能保证$O(\log{n})$的平均复杂度。
B Tree
B树不属于BST,而是一种平衡多路查找树。
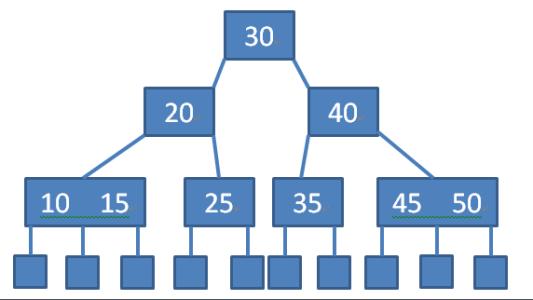
对于多路查找树,一个具有$m$个子节点的父节点,易得有$m-1$个值与$m$个查找方向(区间)相对应。由此给出$m$阶B树的性质:
-
根节点至少有两个子节点;
-
除根节点外,其他节点至少有$ceil(m/2)$个子节点;
-
所有节点最多有$m$个子节点,所有节点存储value的数目等于子节点数目$-1$;
-
所有叶节点都在同一层,并且都为空。
可以看到B树与BST的最大区别就在于$2$路变成了$m$路,B树解决了BST在查找时IO效率低下的问题。BST每个节点只存储一个value,在查找一批数据时会引起大量的IO操作;而B树每个节点可以存储多个值,将B树设置为每个节点最大可以存储一个磁盘块的数据,那么根据局部性原理,将大大提高IO的效率。
对B树的插入与删除操作分别会引起节点的分裂与合并。
B+ Tree
B+树是B树的一个变种,这里只将与B树的区别:
-
B+树的所有数据value都存储在叶节点中,非叶节点中只存储索引key;
-
有$k$个子节点的节点中存储了$k$个索引key;
-
所有叶节点使用链表连接起来,形成一个顺序存储结构。
