Seq2Seq
讲到Attention就不得不提NLP领域最经典的Seq2Seq模型架构:
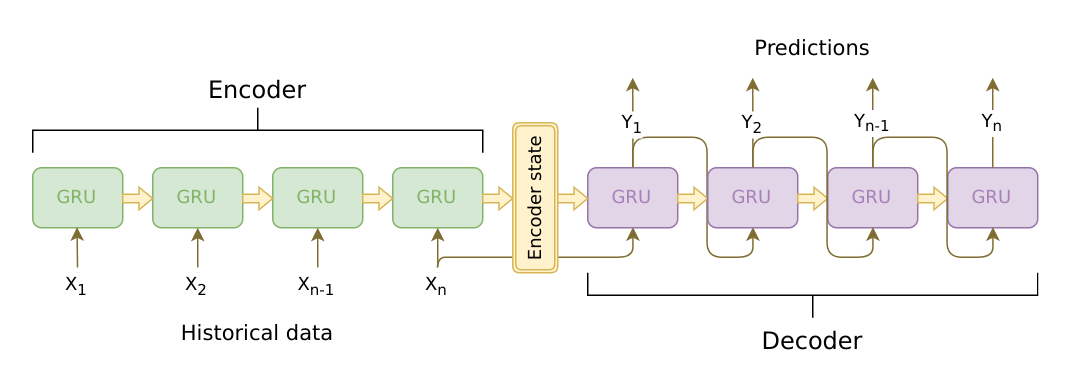
Seq2Seq架构分为两部分,前一部分是编码器(Encoder),后一部分是解码器(Decoder)。以RNN为例(不限于RNN),作为Encoder的RNN负责读入全部输入句子$X$,得到一个上下文向量(Context Vector)。Decoder的作用就是读入这个Context Vec,然后逐步预测$Y$。Seq2Seq架构的优点在于可以处理输入输出端不等长的序列数据,最大的缺点就是把整个序列都压缩到了一个Context Vec中,Decoder要想从单个向量中精确并完整地预测时序信息比较难。
Attention
Bahdanau在2015年首次提出Attention Machanism的概念,原文中叫做Alignment。其思想就是在Decoder解码的过程中,为每一个时刻都计算一个Context Vec。秉着跟论文保持一致的原则,首先对需要用到的变量说明一下。假设Seq2Seq使用LSTM作为RNN单元,那么我们把Encoder每一时刻的输出记作$h_{t}$,而Decoder每一时刻的输出记作$s_{t}$,易得$h$的初始状态是零初始化的,而$h$的最后一个状态会被作为$s$的初始状态。
在Encoder完成编码之后,我们会得到Encoder所有时刻的输出:
\[\vec{h}=\lbrack{h_{1},h_{2},\cdots,h_{T}}\rbrack\]其中$T$表示输入序列$X$的时间长度。然后$h_{T}$作为Decoder的初始状态$s_{0}$,开始解码并输出$s_{1}$。Align Model中每一次decode都需要考虑当前时刻与$X$序列每一个时刻的关系。令Decoder的第$1$时刻与$\vec{h}$各时刻的关系用一个分数向量$\vec{e}_{1}$来表示:
\[\begin{aligned} \vec{e}_{1}&=\lbrack{e_{1,1},e_{1,2},\cdots,e_{1,T}}\rbrack \\ e_{1,i}&=f(s_{0},h_{i}) \\ &=w_{e}\cdot{tanh(w_{s}\cdot{s_{0}}+w_{h}\cdot{h_{i}})} \quad i\in\lbrack{1,T}\rbrack \end{aligned}\]对$\vec{e}{1}$做softmax归一化就可以得到一个和为$1$的权重向量$\vec{\alpha}{1}$:
\[\begin{aligned} \vec{\alpha}_{1}&=\lbrack{\alpha_{1,1},\alpha_{1,2},\cdots,\alpha_{1,T}}\rbrack \\ \vec{\alpha}_{1}&=\frac{\exp(\vec{e}_{1})}{\sum_{T}\exp(\vec{e}_{1})} \\ \end{aligned}\]再将Encoder每个时刻的输出与对应位置的权重相乘再求和,就得到了Decoder该时刻的contex vec:
\[\begin{aligned} c_{1}&=\sum\limits_{T}\vec{h}\cdot\vec{\alpha}_{1} \\ &=\sum\limits_{T}h_{i}\cdot\alpha_{1,i} \\ \end{aligned}\]综上,Attention的运算过程为:
\[\begin{aligned} \vec{e}_{t}&=W_{e}^{T}{\tanh(W_{s}{s_{t-1}}+W_{h}{\vec{h}})} \\ \vec{\alpha}_{t}&=\frac{\exp(\vec{e}_{t})}{\sum_{T}\exp(\vec{e}_{t})} \\ c_{t}&=\left< \vec{\alpha}_{t},\vec{h} \right> \\ \end{aligned}\]Decoder
在此顺带一提运行Decoder的几种策略。
Classic
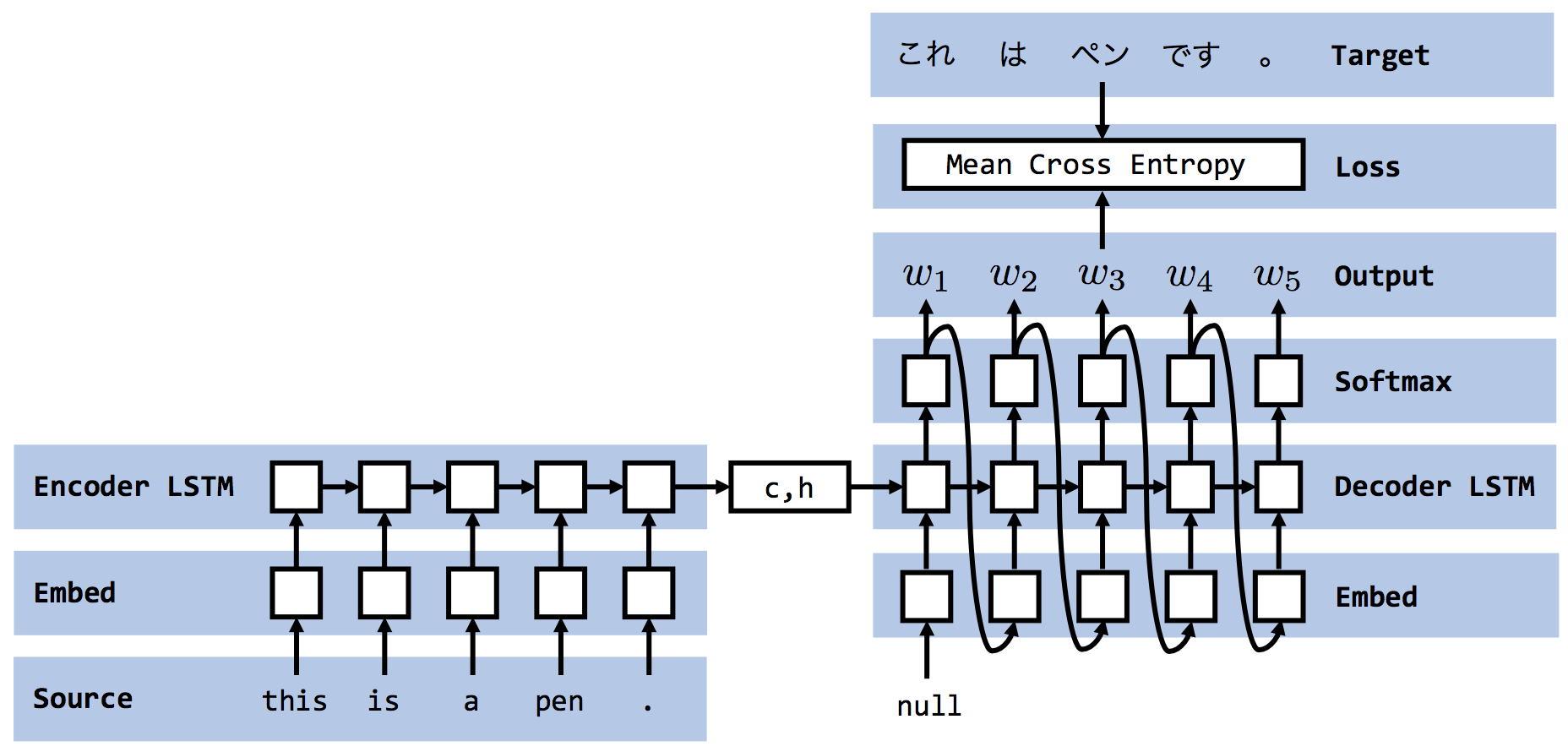
一种是像下图所示,Decoder每一时刻的输入都完全来自于上一时刻的输出。这种方式其实就是经典的RNN训练策略,它有一个明显的缺点,当Decoder某一时刻预测错误时,那么后面时刻的cell只会错的更加离谱。“差之毫厘谬以千里”是对该种方法最好的概括。
Teacher Forcing
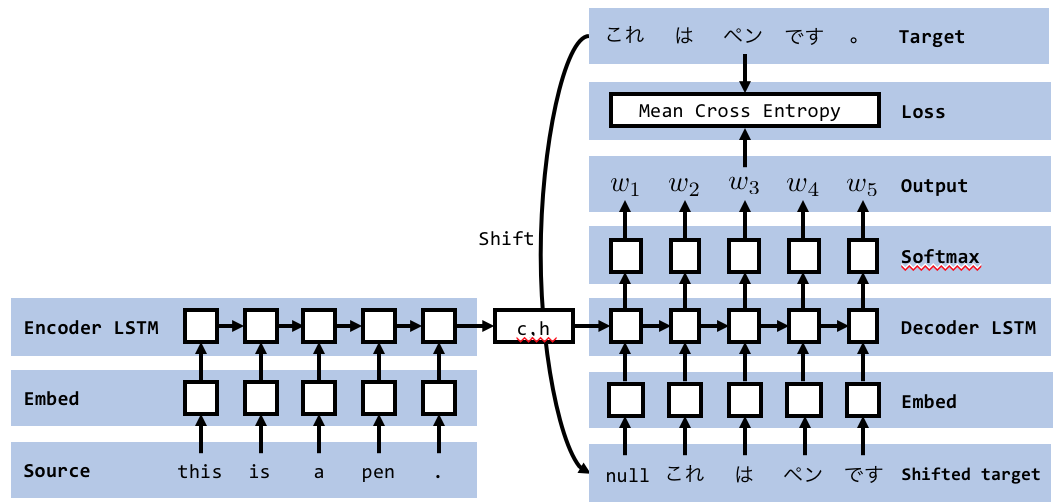
另一种方式就是使用偏移一个单位的真实标签(shifted target)作为输入,如下图所示。这种方法叫做Teacher Forcing,它增强了Decoder训练时的稳定性,能加速模型的收敛。但是该方法无法用于测试(验证),因为测试集的label是不知道的,所以测试模型时还需要换回Classic模式。
BeamSearch
因为Teacher Forcing无法用于模型测试,那么考虑下Classic模式的测试过程。Decoder每个时刻的输出实际上经过了一个argmax运算,即只输出词库中概率最大的那个词。该方法的缺点之前已经提了,就是不稳定,某一个时刻错了后面就会继续错下去。
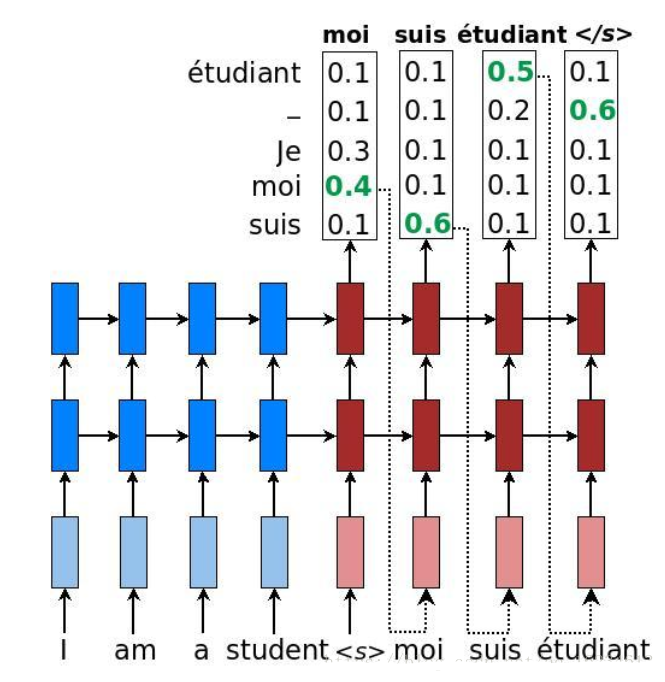
BeamSearch方法改进了这一缺点,使用BeamSearch策略的Decoder每时刻的输出不再局限于单条路线,而是将搜索空间扩大成多条支线。假设BeamSearch的空间参数为$K$,那么Decoder每个时刻都会有$K$个输出,如下图所示。下图是使用BeamSearch策略的Decoder的搜索空间,其中$K=5$。下一时刻的搜索只会选取当前空间的TOP$K$个备选出发,概率不在TOP$K$的就会被抛弃。

Transformer
传统的Seq2Seq模型由于其结构上的缺陷(RNN与CNN),从而没法并行训练。Google在2017年提出一种全新的架构Transfomer,下面就逐步开始讲。
Self-Attention
Transfomer中的关键技术就是Self-Attention机制,论文中将attention机制描述成“一个query和一系列k-v对与输出之间的映射关系”,“输出就是各value的加权和”,而“分配给各value的权重是通过query与各对应的key计算出来的”。
令$x_{i}$表示某个单词的嵌入向量,嵌入维度为$d_{model}$。首先,对一个序列上的每一个$x_{i}$,都乘上$3$个矩阵再次降维得到三个向量,分别令其为Query vector、Key vector和Value vector,其中query和key的维度为$d_{k}$,value的维度为$d_{v}$。
\[\begin{aligned} q_{i}&=x_{i}W^{Q} \\ k_{i}&=x_{i}W^{K} \\ v_{i}&=x_{i}W^{V} \\ \end{aligned}\]易得三个降维矩阵的形状分别为$shape(W^{Q})=shape(W^{K})=(d_{model},d_{k})$,$shape(W^{V})=(d_{model},d_{v})$。
\[z_{i}=\sum\limits_{j=1}^{l}softmax(\frac{q_{i}k_{j}}{\sqrt{d_{k}}})v_{j}\]然后推广到矩阵形式,令序列长度为$l$,先计算位置$x_{i}$上的attention向量。
\[\begin{aligned} shape(x_{i})&=(1,d_{model}) \\ shape(q_{i})&=(1,d_{k}) \\ shape(K)&=(l,d_{k}) \\ shape(V)&=(l,d_{v}) \\ \end{aligned}\]首先将$q_{i}$与所有位置上的$k_{i}$做内积,得到每一个位置上的分数:
\[shape(q_{i}K^{T})=(1,l)\]除以$\sqrt{d_{k}}$后经$softmax$归一化,最后计算每一个位置上的value加权和:
\[\begin{aligned} Attention(q_{i},K,V)&=softmax(\frac{q_{i}K^{T}}{\sqrt{d_{k}}})V \qquad shape:(1,d_{v}) \\ Attention(Q,K,V)&=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V \qquad shape:(l,d_{v}) \\ \end{aligned}\]Multi-Head Attention
为了解决一词多义的问题,Transfomer还提出了改进的Attention机制:Multi-Head Attention。通过同时设置多组$(W^{Q},W^{K},W^{V})$,实现将一个嵌入向量$x_{i}$映射到多个子空间,即在某一位置上得到多个attention向量${z_{i}^{1},\cdots,z_{i}^{h}}$。把同一个位置的多组attention向量拼接起来再乘上一个降维矩阵$W^{O}$就得到了最终的attention向量:
\[MultiHead(Q,K,V)=Concat(Z^{1},\cdots,Z^{h})W^{O}\]Positional Encoding
RNN和序列模型的优势就在于考虑了序列中不同元素的位置信息,Transfomer在首个encoder与decoder处引入了位置编码技术,对每一个位置元素的嵌入向量$x_{i}$,都会加上一个等长的位置向量PE。在原论文中$x_{pos}$对应的PE由两个三角函数确定:
\[\begin{aligned} PE_{pos,2i}&=\sin\frac{pos}{10000^{2i/d_{model}}} \\ PE_{pos,2i+1}&=\cos\frac{pos}{10000^{2i/d_{model}}} \\ \end{aligned}\]其中$pos$表示序列中的第$pos$个元素,而$i$表示向量中的第$i$位。
Architecture
Transfomer在整体上还是一个Encoder-Decoder架构,并且Encoder端与Decoder端有略微的不同。
Encoder端比较简单,就是:
Encoder = (Multi-Head Attention Layer + Feed-Forward Layer) * N
但是第一个Encoder的输入需要加上PE。一个Transfomer中会包含$N$个堆叠的Encoder,Encoder端最终的输出为$K$跟$V$,会被缓存。
然后是Decoder端,同样的,第一个Decoder的输入也是加上PE的嵌入向量。Decoder比Encoder多一层,通常叫做Encoder-Decoder Attention Layer,该层计算的是Decoder某一时刻的query与缓存$K$、$V$的attention向量,该层其实相当于Seq2Seq中的attention机制。然后Decoder端的Multi-Head Attention计算也与Encoder端不同,因为Decoder负责解码,未来时刻的信息不能参与计算,所以需要使用掩码来屏蔽当前位置之后的信息,称为Masked Multi-Head Attention。
Decoder = (Masked Multi-Head Attention Layer + Encoder-Decoder Attention Layer + Feed-Forward Layer) * N
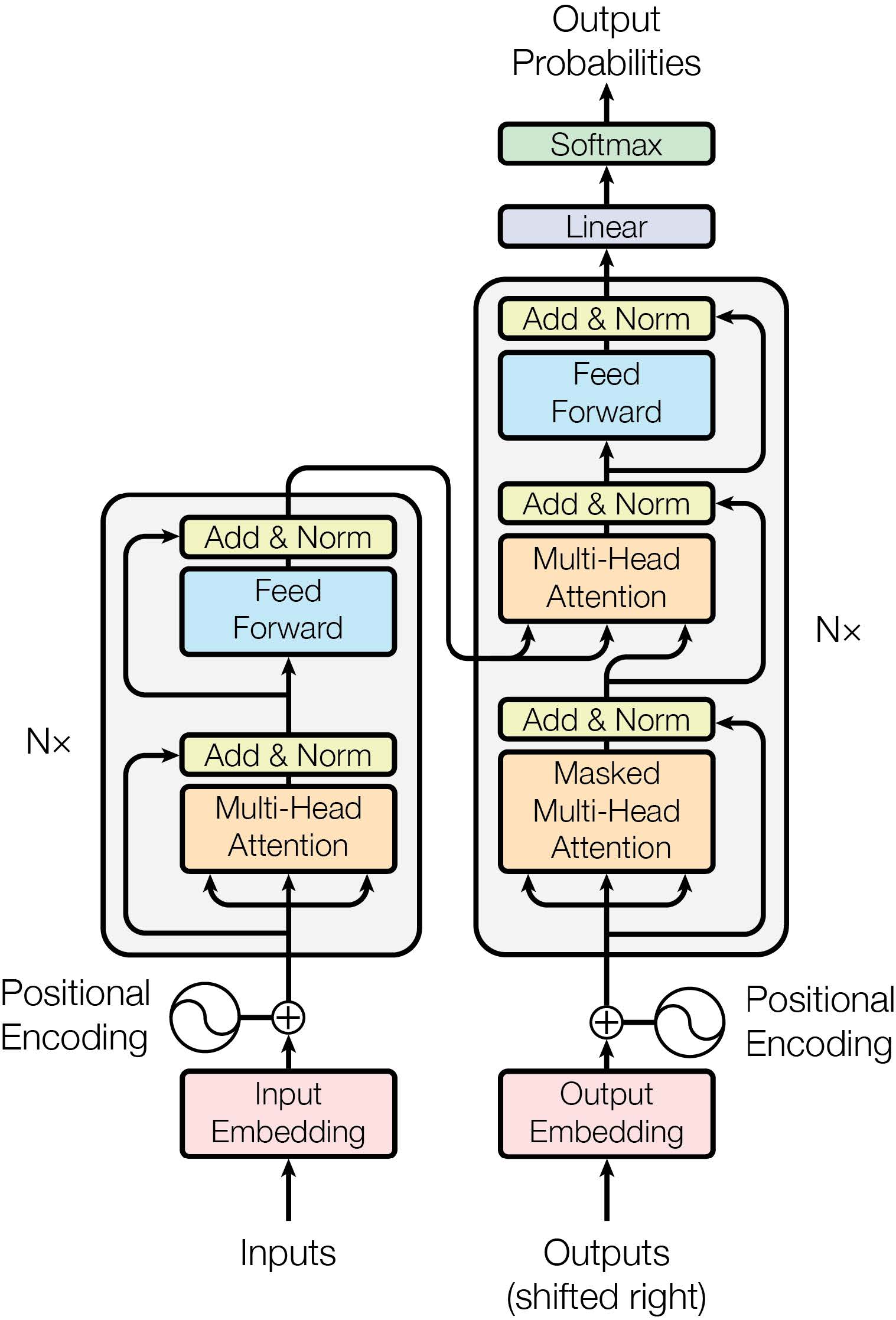
一个Transfomer的架构图如下所示(图源论文):