概述
在实际实现GAN的时候才发现GAN的训练有好多坑,暂不表。
GAN
对抗生成网络(Generative Adversarial Network)将博弈思想引入了神经网络的训练过程,GAN由两个网络模型构成:generator(G)和discriminator(D),前者是一个生成模型,后者是一个判别模型。整个GAN的的训练过程是联合训练两个网络G和D,GAN的网络框架如下图所示:
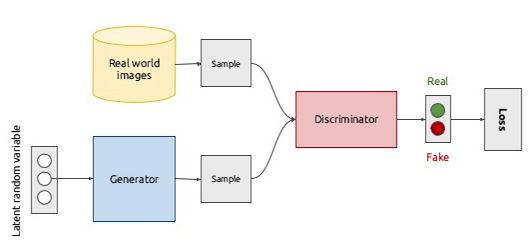
Discriminator
GAN中D的任务很简单,就是判别数据是真是假,即D可以看做是一个二分类器。对于一个输入数据$x$,D会给出其对该数据的打分$D(x)$,该分值越大说明数据$x$为真的可能性越大,反之说明$x$是一个伪造数据。
Generator
生成器的原理可以参考之前的变分自编码文章。简单来说,假设真实数据都是从一个隐变量分布$P(z)$中采样生成的,那么现实世界中任何的数据都可以表示成$f(P(z))$,其中$f(x)$为隐变量到数据的一个转换函数。生成模型的目标就是要学得真实数据与隐变量之间的一个映射关系$f(x)$。
GAN的思想很简单,首先假设生成模型所生成的数据服从一个隐变量分布$P_{g}$,真实数据分布为$P_{r}$。GAN的目标有两个:D要能区分出真实数据与伪造数据,即$f(P_{g}(z_{fake}))$与$f(P_{r}(z_{real}))$之间的区别;G要能产生骗过D的生成数据。换句话说,优化目标有两个:
- 最小化判别器对混合数据的判别损失(判别器角度)
- 最大化判别器对伪造数据的判别损失(生成器角度)
易得$x_{real}=f(P_{r}(z_{real}))$,$x_{fake}=f(P_{g}(z_{fake}))$,那么GAN的损失函数可以写成:
\[\min\limits_{G}\max\limits_{D}V(D,G)=\mathbb{E}_{x\sim{P_{r}}}[\log{D(x)}]+\mathbb{E}_{x\sim{P_{g}}}[\log{(1-D(x))}]\]下面推导优化过程:
\[\begin{aligned} V(D,G)&=\mathbb{E}_{x\sim{P_{r}}}[\log{D(x)}]+\mathbb{E}_{x\sim{P_{g}}}[\log{(1-D(x))}] \\ &=\int_{x}P_{r}(x)\log{D(x)}\,dx+\int_{x}P_{g}(x)\log(1-D(x))\,dx \\ \end{aligned}\]首先是$\max\limits_{D}V(D,G)$,令上述导数为零求出最优判别器:
\[\begin{aligned} \frac{\partial{V(D,G)}}{\partial{D}}&=\frac{P_{r}}{D}-\frac{P_{g}}{1-D}=0 \\ D^{*}&=\frac{P_{r}}{P_{r}+P_{g}} \\ \end{aligned}\]代入最优判别器得到新的目标函数:
\[\begin{aligned} V(D^{*},G)&=\int_{x}P_{r}\log\frac{P_{r}}{P_{r}+P_{g}}+P_{g}\log\frac{P_{g}}{P_{r}+P_{g}}\,dx \\ &=\int_{x}P_{r}\log\frac{P_{r}}{2\frac{P_{r}+P_{g}}{2}}+P_{g}\log\frac{P_{g}}{2\frac{P_{r}+P_{g}}{2}}\,dx \\ &=\int_{x}P_{r}\log\frac{P_{r}}{\frac{P_{r}+P_{g}}{2}}+P_{g}\log\frac{P_{g}}{\frac{P_{r}+P_{g}}{2}}\,dx-2\log{2} \\ &=KL(P_{r}\vert\vert(P_{r}+P_{g}))+KL(P_{g}\vert\vert(P_{r}+P_{g}))-2\log{2} \\ &=2JS(P_{r}\vert\vert{P_{g}})-2\log{2} \\ \end{aligned}\]$\min\limits_{G}V(D^{},G)$等价于$\min{JS(P_{r}\vert\vert{P_{g}})}$,最优解$G^{}$为$P_{r}=P_{g}$。
最后,在GAN的实现上,D与G是交替训练的,每一轮只训练其中一个网络。具体过程如下:
- 固定G的参数,取一批真实图片$X_{r}$,再生成一批伪造图片$X_{g}$,训练D的分辨能力;
- 固定D的参数,取一批真实图片$X_{r}$,再生成一批伪造图片$X_{g}$,训练D的伪造能力。
一个简单的GAN实现见此。
Problem
GAN因为包含两个互相交互的网络,在训练上非常困难。设想一下GAN最初的情况,D只能产生随机噪声,因此即使是一个结构件的G也能很轻易的分辨real与fake数据。主要问题有两个:
- Mode collapse: 模式崩塌。指G只学到了真实数据中的某一部分潜在分布,因而导致G只能生成部分样本种类或单种类样本。如在MNIST数据及上表现为只能生成数字$1$或数字$8$。
- Unbalance: 不平衡。指D与G之间的不平衡,其中一者的能力过强而导致另一者无法再学到东西。这种情况与GAN的思想不符,一个优秀的GAN应该满足两者互相制衡。