Recurrent Neural Network
概述
首先看一下普通前馈神经网络与循环神经网络(Recurrent Neural Network)的对比图:
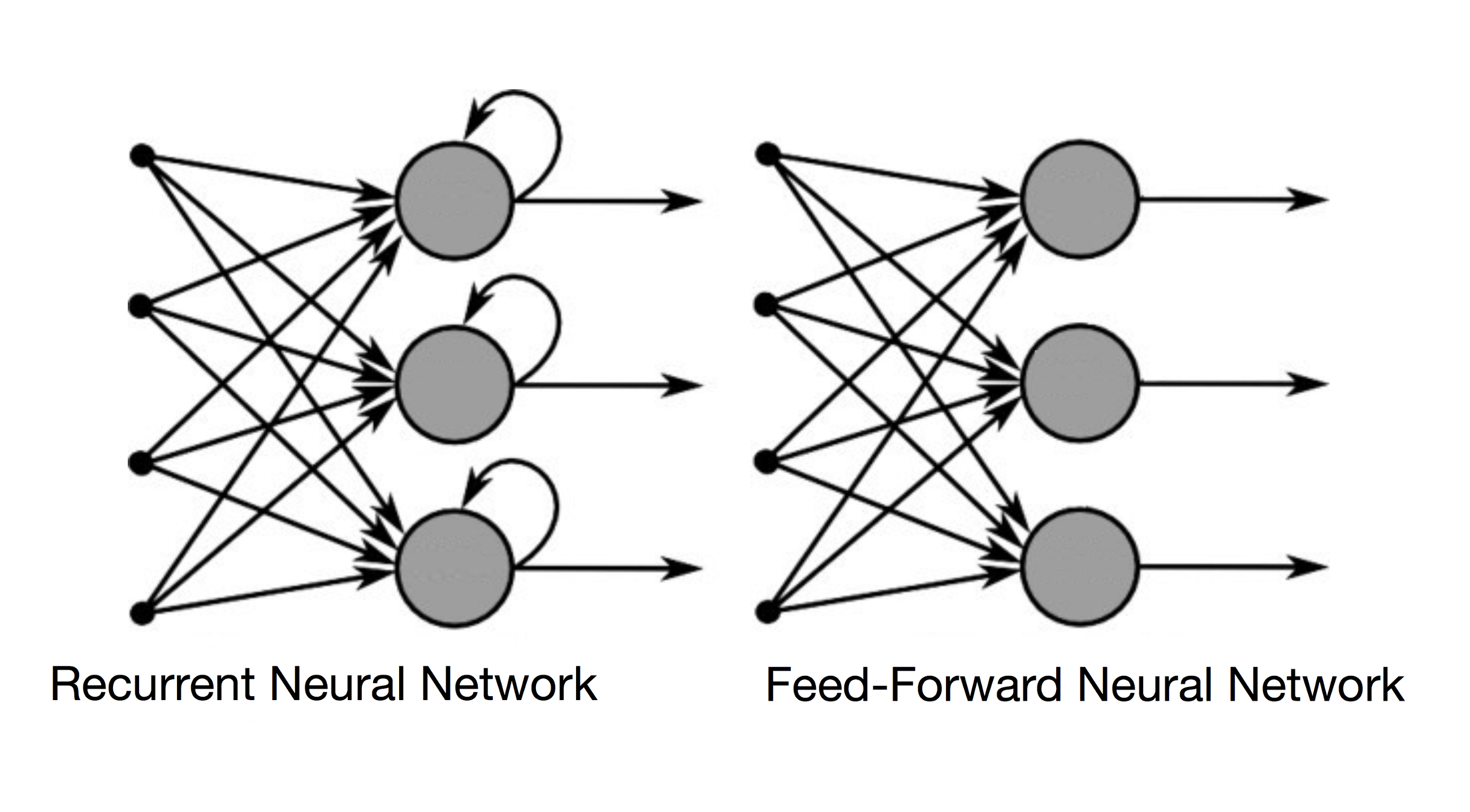
对于普通的前馈神经网络,每一层的计算都可以写成:
\[a^{[i]}=g(a^{[i-1]}\theta^{[i-1]}+b^{[i-1]})\]其中$g(x)$为激活函数,特别地,$a^{[0]}$即为输入$x$,$a^{[-1]}$即为输出$y$。现在假设输入数据$x$有了时间状态,如果想要神经网络能捕捉到数据中的时间关系,那么就在每一层中对所有的状态都计算一次。若数据有$T$个状态,则每一层神经元的计算次数有$T$次,只有当计算完所有状态后,数据流才会进入下一层神经元。下图是单个RNN神经元对一个样本所有状态的计算示意图:
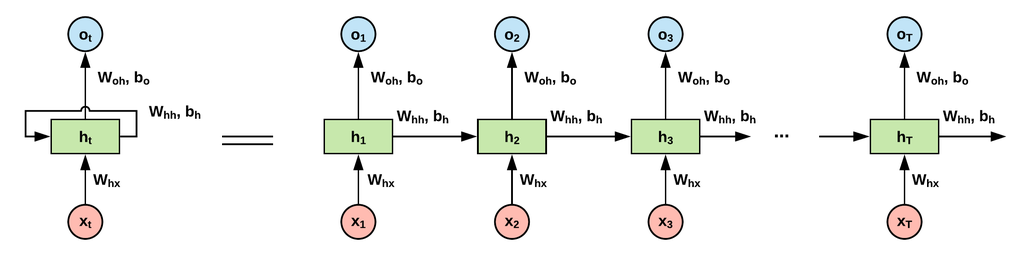
其中$h_{t}$为样本对应状态$x_{t}$的隐藏态,$o_{t}$为样本对应状态$x_{t}$的输出。RNN对这三者默认的计算公式为:
\[\begin{aligned} h_{t}&=tanh(x_{t}W_{x}+h_{t-1}W_{h}+b_{h}) \\ o_{t}&=h_{t}W_{o}+b_{o} \\ \end{aligned}\]注意同一层网络下不同状态的计算是共享参数的,即参数是无状态的。三个权重矩阵的维度分别为:
\[\begin{aligned} W_{x}&=(x,h) \\ W_{h}&=(h,h) \\ W_{o}&=(h,y) \\ \end{aligned}\]RNN相对于DNN的变化不止于此,首先是前向传播过程。DNN前向传播的任务是计算一个$\hat{y}$然后求出模型在该样本上的$loss$;而RNN因为引入了时间状态,输出也可能是多状态的,所以对于每一个$\hat{y}{t}$,都需要计算一个$loss{t}$,然后模型对该样本$x$的损失是所有状态损失的求和:
\[\sum_{t=1}^{T}loss_{t}\]然后考虑反向传播,需要计算的参数有三组,$param_{x}$、$param_{h}$跟$param_{h}$。注意在DNN中,如果网络层数过深会导致梯度消失或梯度爆炸的问题,观察RNN,由于时间因素的引入,每一层的循环计算相当于变相的加深了神经网络的层数,所以该问题在RNN中尤为明显,一般会使用梯度截断或更换激活函数来解决。其次是梯度的计算,由于参数是无状态的,所以同一层网络下的参数梯度是该层所有状态梯度流的加和,同时参数$param_{h}$的梯度是有多个来源的,一个是$h_{t+1}$,另一个是$o_{t}$。
一个基于numpy的mini_char_RNN实现见此。
一个简单的序列预测RNN实现见此。
RNN的记忆特性并不是说RNN只能处理序列型数据,如果把图片的行看做是特征,将列看做是时间轴,那么RNN也能用于处理图片。比如一个最简单的矩阵:
\[x= \left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix} \right]\]将不同行看成是样本在不同时间下的不同状态,那么有$x_{t_{1}}=[1 \quad 2]$,$x_{t_{2}}=[3 \quad 4]$,把图片逐行的送入RNN进行计算,可以实现利用RNN来做图像处理。
一个RNN做图像分类的示例见此。
LSTM
RNN的优劣很明显,优点就是把之前状态的信息加入了计算,缺点就是变相加深了网络的层数。那么随着网络层数的加深,问题也随之而来。一是状态信息会随着时间轴的推进而慢慢缩小,导致与预测目标相距太远的状态信息起不到多少作用;二是深层网络的梯度消失/爆炸现象更容易发生。
为了解决梯度消失的问题,LSTM被推出,其单元结构如下图所示(图源Udacity):
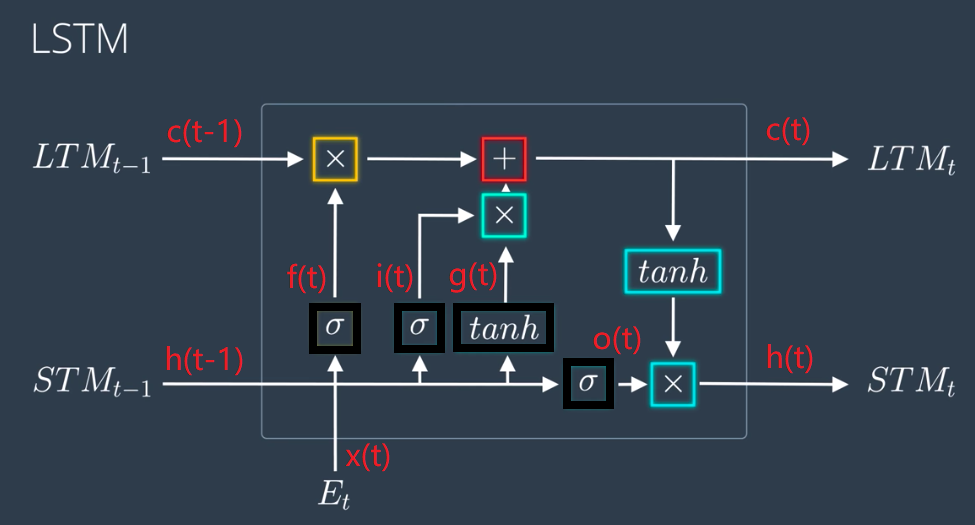
LSTM使用门结构(sigmoid)来控制单元内的信息流动,并且加入了长/短期记忆的概念。这里用黑框标注了四个主要操作,具体的门结构构成为:
- 遗忘门(forgot gate):$f(t)$,决定之前的长期记忆需要遗忘还是保留
- 输入门(input gate):$i(t)$,决定当前的短期记忆是否需要加入到长期记忆中
- 输出门(output gate):$o(t)$,短期记忆的传递
上图中的标识只是为了便于理解,加上去的红字标注才是更大众化的表示。其中$g(t)$不是门结构,但是$g(t)$计算的是候选状态$\widetilde{c}(t)$。一个LSTM单元针对四个操作就分别对应有四组参数,而每组参数又需要对$x$与$h$做区分,所以每个LSTM就有八个不同的权重系数,在实践中具体的参数如下:
- $W_{fx}$,$W_{fh}$,$b_{f}$
- $W_{ix}$,$W_{ih}$,$b_{i}$
- $W_{gx}$,$W_{gh}$,$b_{g}$
- $W_{ox}$,$W_{oh}$,$b_{o}$
明确参数之后LSTM单元内部的门运算为:
\[\begin{aligned} f(t)&=\sigma(x_{t}W_{fx}+h_{t-1}W_{fh}+b_{f}) \\ i(t)&=\sigma(x_{t}W_{ix}+h_{t-1}W_{ih}+b_{i}) \\ o(t)&=\sigma(x_{t}W_{ox}+h_{t-1}W_{oh}+b_{o}) \\ \end{aligned}\]其状态变化为:
\[\begin{aligned} \widetilde{c}(t)&=tanh(x_{t}W_{gx}+h_{t-1}W_{gh}+b_{g}) \\ c&:=f\times{c}+i\times{\widetilde{c}} \\ h&:=o\times{tanh(c)} \\ \end{aligned}\]一个简单的LSTM层实现见此。
GRU
GRU是LSTM的一种变体,相较于LSTM中的输入门、遗忘门、输出门,GRU中只有两个门:
- 重置门(reset gate):$r(t)$,
- 更新门(update gate):$z(t)$,
每个cell内部的门计算为:
\[\begin{aligned} z(t)&=\sigma(x_{t}W_{zx}+h_{t-1}W_{zh}+b_{z}) \\ r(t)&=\sigma(x_{t}W_{rx}+h_{t-1}W_{rh}+b_{r}) \\ \end{aligned}\]GRU状态变化为:
\[\begin{aligned} c(t)&=tanh(x_{t}W_{cx}+r(t)\times{h_{t-1}W_{ch}}) \\ h_{t}&=(1-z)\times{h_{t-1}}+z\times{c} \\ \end{aligned}\]Highway Network
公路网络(Highway Network)受LSTM的启发,同样引入了门机制(gating mechanism)来限制数据在网络中的流动。
假设普通神经网络中的非线性变换为:
\[y=H(x)\]其中$H(x)$为激活函数。
公路网络引入了一个transform gate $T(x)$,还有一个carry gate $1-T(x)$,公路网络中每一层的输出为:
\[y=H(x)\cdot{T(x)}+x\cdot{(1-T(x))}\]