LDA
单变量二分类
假设现在有一个单变量二分类问题,并且标签服从二项分布,特征条件概率服从等方差的高斯分布:
\[P(y=1)=\phi \\ P(y=0)=1-\phi \\ P(x|y=1)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x-\mu_{1})^{2}}{2\sigma^{2}}] \\ P(x|y=0)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x-\mu_{0})^{2}}{2\sigma^{2}}] \\\]那么在给定样本的条件下,这两个类别发生的条件概率分别为:
\[P(y=1|x)=\frac{P(y=1)P(x|y=1)}{P(y=0)P(x|y=0)+P(y=1)P(x|y=1)} \\ P(y=0|x)=\frac{P(y=0)P(x|y=0)}{P(y=0)P(x|y=0)+P(y=1)P(x|y=1)} \\\]两者之间的对数几率可以写成:
\[\begin{aligned} \log\frac{P(y=1|x)}{P(y=0|x)}&=\log\frac{P(y=1)}{P(y=0)}+\log\frac{P(x|y=1)}{P(x|y=0)} \\ &=\log\frac{\phi}{1-\phi}+\log\frac{exp[-\frac{(x-\mu_{1})^{2}}{2\sigma^{2}}]}{exp[-\frac{(x-\mu_{0})^{2}}{2\sigma^{2}}]} \\ &=\log\frac{\phi}{1-\phi}-\frac{(x-\mu_{1})^{2}}{2\sigma^{2}}+\frac{(x-\mu_{0})^{2}}{2\sigma^{2}} \\ &=\frac{\mu_{1}-\mu_{0}}{\sigma^{2}}{\cdot}x-\frac{\mu_{1}^{2}-\mu_{0}^{2}}{2\sigma^{2}}+\log\frac{\phi}{1-\phi} \end{aligned}\]由上式可以得到,LDA对于某一样本的线性判别函数可写成:
\[\delta_{1}(x)=\frac{\mu_{1}}{\sigma^{2}}{\cdot}x-\frac{\mu_{1}^{2}}{2\sigma^{2}}+\log{\phi} \\ \delta_{0}(x)=\frac{\mu_{0}}{\sigma^{2}}{\cdot}x-\frac{\mu_{0}^{2}}{2\sigma^{2}}+\log{(1-\phi)} \\\]单变量多分类
不难得到,对于多分类问题,LDA模型的预测输出为:
\[\begin{aligned} f(x)&=\arg\max\limits_{k}\delta_{k}(x) \\ &=\arg\max\limits_{k} \ \frac{\mu_{k}}{\sigma^{2}}{\cdot}x-\frac{\mu_{k}^{2}}{2\sigma^{2}}+{\log}p_{k} \end{aligned}\]其中$p_{k}$为类分布概率。
多变量多分类
更一般的,讨论多变量的情况下,假如数据$X$有$p$个特征,在$y=k$的条件下,引入协方差矩阵,特征条件概率可以写成:
\[P(x|y=k)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu_{k})^{T}\Sigma^{-1}(x-\mu_{k}))\]线性判别函数为:
\[\delta_{k}(x)=x^{T}\Sigma^{-1}\mu_{k}-\frac{1}{2}\mu_{k}^{T}\Sigma^{-1}\mu_{k}+{\log}p_{k}\]LDA模型的预测输出为:
\[\begin{aligned} f(x)&=\arg\max\limits_{k}\delta_{k}(x) \\ \end{aligned}\]其中各参数均由观测数据估计得到:
- $\hat{p}{k}=\frac{N{k}}{N}$,$N_{k}$为某个类别的样本数,$N$为总样本数
- $\hat{\mu}{k}=\frac{1}{N{k}}\sum_{x{\in}C_{k}}x_{i}$,$C_{k}$表示第\(k\)个类别的样本集合
- $\hat{\Sigma}=\frac{1}{N-K}\sum_{k=1}^{K}\sum_{x{\in}C_{k}}(x_{i}-\hat{\mu}{k})(x{i}-\hat{\mu}_{k})^{T}$,$K$表示类别数
所以可以看出LDA就是一个简单的贝叶斯模型,并没有用到最大似然策略。
QDA
LDA模型有一个前提假设:数据的特征条件概率服从均值不等、方差相等的高斯分布,如果真实情况下方差不等呢?下图展示了方差相等于方差不等的情况:
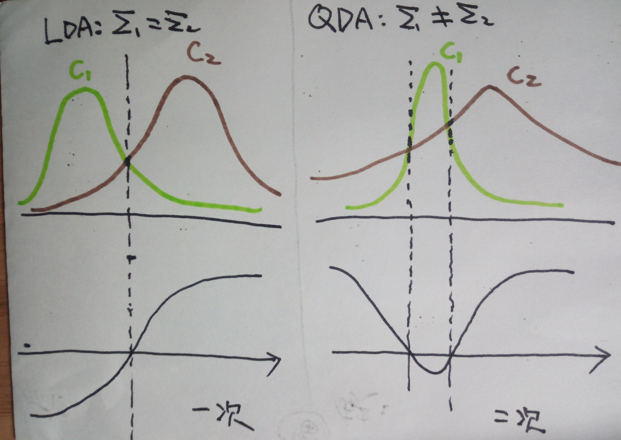
同理,可以得到QDA(quadratic discriminant analysis)的判别函数:
\[\delta_{k}(x)=-\frac{1}{2}\log|\Sigma_{k}|-\frac{1}{2}(x-\mu_{k})^{T}\Sigma_{k}^{-1}(x-\mu_{k})+{\log}p_{k}\]QDA模型的预测输出为:
\[\begin{aligned} f(x)&=\arg\max\limits_{k}\delta_{k}(x) \\ \end{aligned}\]其中各参数均由观测数据估计得到:
- $\hat{p}{k}=\frac{N{k}}{N}$,$N_{k}$为某个类别的样本数,$N$为总样本数
- $\hat{\mu}{k}=\frac{1}{N{k}}\sum_{x{\in}C_{k}}x_{i}$,$C_{k}$表示第$k$个类别的样本集合
- $\hat{\Sigma}{k}=\frac{1}{N{k}-1}\sum_{x{\in}C_{k}}(x_{i}-\hat{\mu}{k})(x{i}-\hat{\mu}_{k})^{T}$.
Fisher角度解析LDA
待补充,这部分没太理解
LDA用于降维
对于$K$个类别的数据,假定“物以类聚”的条件成立,那么对于$K$个中心,在不影响分类器性能的条件下,我们至少可以将其映射到一个$K-1$维的空间。如对于两个聚类中心,我们可以将其映射到一条直线上并且还能将其分开,对于$K>3$的情况,可以找到一个$L<K-1$维的映射空间。所以LDA算法还有一个用途就是作为有监督的降维算法,其核心思想在于将原数据映射到一个新空间,使得在新空间中各类的均值差尽量大,而每个类内部的方差尽量小,那么在二分类的情况下很容易给出一个直观的优化目标:
\[\max \frac{(\mu_{1}-\mu_{2})^{2}}{\sigma_{1}^2+\sigma_{2}^{2}}\]为了将概念拓展到高维空间,首先给出几个概念:
- 类间(between-class)散度矩阵:$S_{b}=\sum\limits_{i=k}^{K}N_{k}(\mu_{k}-\mu)(\mu_{k}-\mu)^{T}$,其中$\mu_{k}$为类均值,$\mu$为数据均值
- 类内(within-class)散度矩阵:$S_{w}=\sum\limits_{k}^{K}\sum\limits_{x_{i}{\in}C_{k}}(x_{i}-\mu_{k})(x_{i}-\mu_{k})^{T}$
在Fisher提出的方法中,降维过程可以写成:
\[Z=a^{T}X\]其中$a$为映射矩阵,$X$为原数据。那么低维数据的类间方差为$a^{T}S_{b}a$,类内方差为$a^{T}S_{w}a$,降维的优化目标就等同于最大化一个瑞利熵:
\[\max\limits_{a}\frac{a^{T}S_{b}a}{a^{T}S_{w}a}\]该优化问题还等价于:
\[\max\limits_{a}a^{T}S_{b}a \qquad s.t. \ a^{T}S_{w}a=K\]使用拉格朗日数乘法解上述问题:
\[L(a)=a^{T}S_{b}a-\lambda(a^{T}S_{w}a-K) \\ \frac{\partial{L(a)}}{\partial{a}}=2S_{b}a-2{\lambda}S_{w}a=0 \\ S_{b}a={\lambda}S_{w}a \\\]假设$S_{w}$可逆:
\[S_{w}^{-1}S_{b}a-{\lambda}a=0 \\ (S_{w}^{-1}S_{b}-{\lambda}I)a=0 \\\]可以看到这就是一个特征值问题。