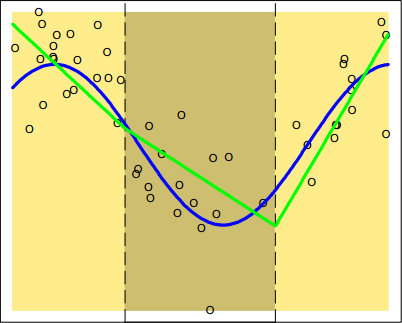
Basis Expansions and Regularization
首先,假定数据$X$有$P$个特征,那么具有$M$项的广义线性模型可以表示成:
\[\begin{aligned} f(X)&=\sum\limits_{m}^{M}\theta_{m}h_{m}(X) \\ &=\theta_{1}h_{1}(X)+\cdots+\theta_{M}h_{M}(X) \\ \end{aligned}\]其中$h_{m}(X)$是对$X$某一特征或某几个特征的变换函数,通常取值如下所示:
- $h_{m}(X)=X_{m}$,直接取出$X$的第$m$个特征;特别地,当$M=P$时,此变换下的模型相当于简单线性模型
- $h_{m}(X)=X_{i}^{2}$,对$X$的某一列做平方变换
- $h_{m}(X)=X_{i}X_{j}$,对$X$的某两列做交互变换
- $h_{m}(X)=\log(X_{i})$,对数变换
- $h_{m}(X)=\sqrt{X_{i}}$,开方变换
- $h_{m}(X)=I(L_{m}{\le}X_{i}<U_{m})$,指示$X$的某一列是否属于指定区间
分段与样条
在上述表达式中,当$h_{m}(X)$取指示函数$I(L_{m}{\le}X_{i}<U_{m})$时,就转变成了分段多项式拟合或者叫样条,一个简单的示例如下:
\[\begin{aligned} f(X)&=\theta_{1}I(X<\xi_{1})+\theta_{2}I(\xi_{1}{\le}X<\xi_{2})+\theta_{3}I(\xi_{2}{\le}X) \\ &=\begin{cases} \theta_{1}, \qquad X<\xi_{1} \\ \theta_{2}, \qquad \xi_{1}{\le}X<\xi_{2} \\ \theta_{3}, \qquad \xi_{2}{\le}X \\ \end{cases} \end{aligned}\]上式将$X$的区间划成了三部分,三部分的模型参数只能使用目标变量的均值来估计,即$\theta_{i}=\bar{Y}_{i}$,模型的拟合图如下图所示:
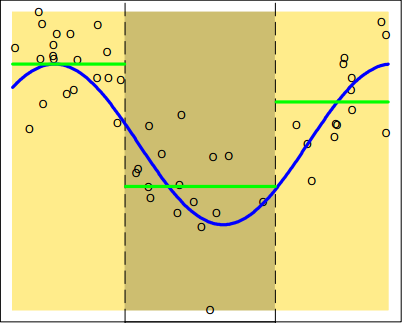
这称为分段常数拟合。有分段常数拟合就肯定有分段线性拟合,把上式改写成:
\[\begin{aligned} f(X)&=\theta_{1}I(X<\xi_{1})+\theta_{2}I(\xi_{1}{\le}X<\xi_{2})+\theta_{3}I(\xi_{2}{\le}X)+ \\ & \quad \theta_{4}I(X<\xi_{1})X+\theta_{5}I(\xi_{1}{\le}X<\xi_{2})X+\theta_{6}I(\xi_{2}{\le}X)X \\ &=\begin{cases} \theta_{1}+\theta_{4}X, \qquad X<\xi_{1} \\ \theta_{2}+\theta_{5}X, \qquad \xi_{1}{\le}X<\xi_{2} \\ \theta_{3}+\theta_{6}X, \qquad \xi_{2}{\le}X \\ \end{cases} \end{aligned}\]模型拟合图如下图所示:
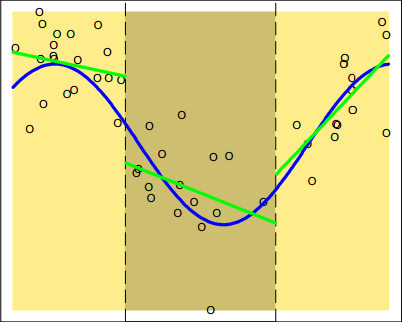
这是分段线性拟合,可以看出这其实相当于使用三个独立的简单线性模型去拟合一个较复杂的多项式关系。特别地,如果再令模型在整个区间上是连续的,那么会得到一个连续分段线性拟合模型: