模型概述
首先回顾一下Logistic Regression,对于一组数据$X$与标签$Y$,Logistic Regression的任务是要找到一组参数使得$X\theta^{T}=threshold$,对于$x\theta^{T}\lt{threshold}$的样本判定为负样本,而对于$x\theta^{T}\gt{threshold}$的样本判定为正样本,其是一个线性分类器。问题在于,如果有一个理想数据集线性可分,那么模型会因为参数的不同而具有不同的决策边界,那么在这些决策边界中如何判定孰优孰劣?
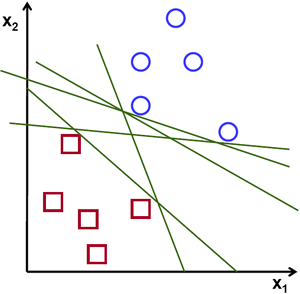
对于Logistic Regression这种概率模型而言,在给定一个确定的threshold之后,就可以画出其决策边界,空间中的样本点离决策边界越远,说明模型对该样本的判定可信度越高。那么,在若干决策边界中,只需要找到一个决策边界,使得模型对两个类别的判定可信度均最高即可获得一个最优分类器。由此引出支持向量机(Support Vector Machine):
数据集$X=[x^{(1)},x^{(2)},…,x^{(m)}]^{T}$,标签$Y=[y^{(1)},y^{(2)},…,y^{(m)}]\in{+1,-1}$,为了实现分类的目的,需要找到一组参数满足$x\theta^{T}+\theta_{0}=0$,同时还需要满足$X$中的各样本点离决策边界$x\theta^{T}=0$的距离最远。
SVM模型对未知样本的预测计算如下:
\[\hat{y}= \left\{ \begin{aligned} &+1, &\hat{x}\theta^{T}+\theta_{0}\ge+1\\ &-1, &\hat{x}\theta^{T}+\theta_{0}\le-1 \\ \end{aligned} \right.\]换句话说,SVM模型的决策边界实际上是由两条直线决定的:
\[x\theta^{T}+\theta_{1}=+1 \\ x\theta^{T}+\theta_{2}=-1\]在训练数据集中,满足以上直线方程的样本点就被称为支持向量(support vector)。根据平行直线距离公式 \(\frac{|C_{1}-C_{2}|}{\sqrt{A^{2}+B^{2}}}\) 得这两条直线之间的距离为: \(d=\frac{2}{||\theta||_{2}}\)
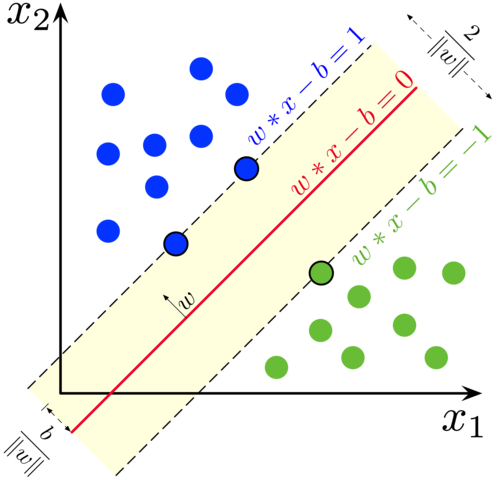
对分类任务而言,还需要满足分类的准确性,假设数据是线性可分的,则有:
\[y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1\]所以SVM可以用如下表达式来描述:
\[\theta^{*}=\arg\max\limits_{\theta} \ \frac{2}{||\theta||_{2}}, \qquad s.t. \ y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1,i=1,...m\]上式等价于:
\[\theta^{*}=\arg\min\limits_{\theta} \ \frac{1}{2}||\theta||_{2}, \qquad s.t. \ y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1,i=1,...m\]容易看出SVM自带参数正则化。
接下来看一下SVM的损失函数,SVM只关心那些被误分的点,而对于正确分类的点是不计入loss的,由几何知识易得,模型对被正确分类的点的输出总是满足:$y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1$,所以SVM的损失函数可以写成:
\[Loss_{SVM}=\frac{1}{2}||\theta||_{2}+max(0,1-y(x\theta+\theta_{0}))\]以上是数据可分的情况,那么如果数据不可分呢?那么允许某些预测样本不一定要严格在直线外侧,允许某些样本处于直线的内侧,那么这些被“容忍”的样本就不满足$y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1$了,为了量化这些被“容忍”的样本偏离正轨的程度,为每一个样本引入一个松弛变量(slack variables)$\xi_{i}$,这些样本需要满足的条件就变为下式:
\[y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1-\xi_{i}\]很显然$\xi_{i}\ge0$,并且该变量体现了模型允许样本越界的程度。那么自然而然地会想到这个越界程度不能是无限制的,所以还要对该变量进行限制,因此SVM问题就变成:
\[\begin{aligned} \theta^{*}=\arg\min\limits_{\theta} \ \frac{1}{2}||\theta||_{2}+C\sum_{i=1}^{m}\xi_{i}, \qquad s.t.& \ y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1-\xi_{i},i=1,...m \\ & \ \xi_{i}\ge0,i=1,...m \\ \end{aligned}\]其中$C$为样本越界的代价系数,其值越大,对越界的惩罚就越大。
最优解
如果我们有如下优化问题:
\[x^{*}=\arg\min\limits_{x}f(x) \qquad s.t. \ g(x)\le0 \\\]那么可以使用拉格朗日数乘法来得到一个拉格朗日函数:
\[L(x,\lambda)=f(x)+{\lambda}g(x)\]其中$\lambda>0$。现考虑针对参数$\lambda$最大化该函数:
\[\lambda^{*}=\max\limits_{\lambda}L(x,\lambda)=f(x)+\max\limits_{\lambda}{\lambda}g(x)\]注意到$\lambda>0$,$g(x)\le0$,所以在满足原问题约束条件的情况下,有:
\[L(x,\lambda^{*})=f(x)\]所以原优化问题可以写成:
\[x^{*},\lambda^{*}=\arg\min\limits_{x}\max\limits_{\lambda}L(x,\lambda)\]在解优化问题时,如果目标函数是凸函数,那么就可以很容易得到一个全局最优解。拉格朗日问题还有一个对偶问题:
\[\lambda^{*},x^{*}=\arg\max\limits_{\lambda}\min\limits_{x}L(x,\lambda)\]原问题与对偶问题同解的充要条件为KKT条件:
\[\begin{aligned} \frac{\partial L(x^{*},\lambda^{*})}{\partial x}&=0 \\ {\lambda}^{*}g(x^{*})&=0 \\ g(x^{*})&\le0 \\ \lambda^{*}&\ge0 \\ \end{aligned}\]SVM问题是一个带线性不等式约束的最优化问题:
\[\begin{aligned} \theta^{*},\lambda^{*}&=\arg\min\limits_{\theta}\max\limits_{\lambda}L(\theta,\lambda) \\ &=\arg\min\limits_{\theta}\max\limits_{\lambda}\frac{1}{2}||\theta||_{2}^{2}-\sum_{i=1}^{m}\lambda_{i}[y^{i}\cdot{}(x^{i}\theta^{T}+\theta_{0})-1], \qquad s.t. \ \lambda_{i}\ge0 \end{aligned}\]将其转成对偶问题来解:
\[\begin{aligned} \lambda^{*},\theta^{*}&=\arg\max\limits_{\lambda}\min\limits_{\theta}L(\theta,\lambda) \\ &=\arg\max\limits_{\lambda}\min\limits_{\theta}\frac{1}{2}||\theta||_{2}^{2}-\sum_{i=1}^{m}\lambda_{i}[y^{i}\cdot{}(x^{i}\theta^{T}+\theta_{0})-1], \qquad s.t. \ \lambda_{i}\ge0 \end{aligned}\]令$\frac{\partial{L}}{\partial{\theta}}=\frac{\partial L}{\partial \theta_{0}}=0$得:
\[\begin{aligned} \frac{\partial{L}}{\partial{\theta}}&=\theta-\sum_{i=1}^{m}\lambda_{i}y^{i}x^{i}=0 \\ \frac{\partial{L}}{\partial{\theta_{0}}}&=-\sum_{i=1}^{m}\lambda_{i}y^{i}=0 \\ \theta^{*}&=\sum_{i=1}^{m}\lambda_{i}y^{i}x^{i} \end{aligned}\]将拉格朗日函数展开并代入最优$\theta^{*}$:
\[\begin{aligned} L(\theta^{*},\lambda)&=\frac{1}{2}||\theta^{*}||_{2}-\sum_{i=1}^{m}\lambda_{i}[y^{i}\cdot{}(x^{i}{\theta^{*}}^{T}+\theta_{0})-1] \\ &=\frac{1}{2}||\theta^{*}||_{2}-(\sum_{i=1}^{m}\lambda_{i}y^{i}x^{i})\cdot{\theta^{*}}^{T}-(\sum_{i=1}^{m}\lambda_{i}y^{i})\cdot\theta_{0}+\sum_{i=1}^{m}\lambda_{i} \\ &=\frac{1}{2}\theta^{*}{\theta^{*}}^{T}-\theta^{*}{\theta^{*}}^{T}+\sum_{i=1}^{m}\lambda_{i} \\ &=\sum_{i=1}^{m}\lambda_{i}-\frac{1}{2}\theta^{*}{\theta^{*}}^{T} \\ &=\sum_{i=1}^{m}\lambda_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}\lambda_{j}y^{i}y^{j}x^{i}{x^{j}}^{T} \end{aligned}\]最大化上式即可求出最优化参数$\lambda^{*}$:
\[\lambda^{*}=\arg\max\limits_{\lambda}L(\theta^{*},\lambda), \qquad s.t. \ \sum\limits_{i=1}^{m}\lambda_{i}y^{i}=0\]最优的SVM模型输出为:
\[\begin{aligned} \hat{y}&= \left\{ \begin{aligned} &+1, &\hat{x}(\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}x^{i})^{T}\ge+1\\ &-1, &\hat{x}(\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}x^{i})^{T}\le-1 \\ \end{aligned} \right. \\ &= \left\{ \begin{aligned} &+1, &\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}\langle\hat{x},x^{i}\rangle\ge+1\\ &-1, &\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}\langle\hat{x},x^{i}\rangle\le+1\\ \end{aligned} \right. \end{aligned}\]其中$\hat{x}$表示待预测的样本,$\hat{y}$表示模型对该样本的预测值。回顾一下拉格朗日函数:
\[max \ L(\lambda)=\frac{1}{2}||\theta^{*}||_{2}^{2}-\sum_{i=1}^{m}\lambda_{i}(y^{i}\cdot{}x^{i}{\theta^{*}}^{T}-1), \qquad s.t. \ \lambda_{i}\ge0\]注意到,如果某样本$x^{i}$不是支持向量,那么有$y^{i}\cdot{x^{i}\theta^{T}}-1>0$,为了最大化拉格朗日函数,必定有$\lambda_{i}^{}=0$,即非支持向量对应的$\lambda^{}$均为0,从理论上说明了SVM的决策边界只跟支持向量有关。
核函数
以上讨论都是基于数据集线性可分的假设下,如果数据集在原始维度下线性不可分怎么办?最简单的办法就是为数据集增加高维度特征。假设现在有一个二维数据集:
\[X= \left[ \begin{matrix} x_{1}^{(1)}&x_{2}^{(1)} \\ x_{1}^{(2)}&x_{2}^{(2)} \\ \vdots \\ x_{1}^{(m)}&x_{2}^{(m)} \\ \end{matrix} \right]\]此数据集二维平面上线性不可分,但是在经一个变换函数$\phi(x)$作用下生成的新数据集是线性可分的:
\[\phi(x_{1},x_{2})=(x_{1}^2,\sqrt{2}x_{1}x_{2},x_{2}^2)\]对于升维后的新数据集$\phi(X)$,SVM所做的计算变成了:
\[\begin{aligned} pred&=\sum_{i=1}^{m}\lambda_{i}y^{(i)}\langle\phi(\hat{x}),\phi(x^{(i)})\rangle \\ &=\sum_{i=1}^{m}\lambda_{i}y^{(i)}\langle(\hat{x}_{1}^2,\sqrt{2}\hat{x}_{1}\hat{x}_{2},\hat{x}_{2}^2),({x_{1}^{(i)}}^2,\sqrt{2}x_{1}^{(i)}x_{2}^{(i)},{x_{2}^{(i)}}^2)\rangle \\ &=\sum_{i=1}^{m}\lambda_{i}y^{(i)}(\hat{x}_{1}^{2}{x_{1}^{(i)}}^{2}+2\hat{x}_{1}x_{1}^{(i)}\hat{x}_{2}x_{2}^{(i)}+\hat{x}_{2}^{2}{x_{2}^{(i)}}^{2}) \\ &=\sum_{i=1}^{m}\lambda_{i}y^{(i)}(\hat{x}_{1}x_{1}^{(i)}+\hat{x}_{2}x_{2}^{(i)})^{2} \\ &=\sum_{i=1}^{m}\lambda_{i}y^{(i)}\langle(\hat{x}_{1},\hat{x}_{2}),(x_{1}^{(1)},x_{2}^{(2)})\rangle^{2} \\ &=\sum_{i=1}^{m}\lambda_{i}y^{(i)}\langle\hat{x},x^{(i)}\rangle^{2} \end{aligned}\]通过上面的变换,不难看出,在将数据集升维之后,SVM训练、预测时的计算其实就可以转化为原始特征的计算,那么何必要对数据集进行升维操作呢?
以上述数据集为例,选取一个函数$\kappa(x_{1},x_{2})=\langle{x_{1}},{x_{2}}\rangle^{2}$,用它来代替SVM的内积计算:
\[\hat{y}=\left\{ \begin{aligned} &+1, &\sum_{i=1}^{m}\lambda_{i}y^{i}\kappa(\hat{x},x^{i})\ge+1\\ &-1, &\sum_{i=1}^{m}\lambda_{i}y^{i}\kappa(\hat{x},x^{i})\ge+1\\ \end{aligned} \right.\]这样一来,这个SVM模型的训练、预测过程就等同于在高维空间进行,即达到了线性划分数据集的目的,也没有增加复杂的运算,其中$\kappa(x_{1},x_{2})$被称为核函数(kernel function),这种方法被称为核技巧(kernel trick)。
现实任务中,一般是不知道要对数据应用怎样的升维函数$\phi(x)$才能使得数据集线性可分,那么自然就难以求得计算高维空间的核函数$\kappa(\cdot,\cdot)$,甚至不知道某函数是否能被用作核函数。
简单来说,一个函数要能被当做核函数,需要满足Mercer’s condition,即对称函数$\kappa(\cdot,\cdot)$的核矩阵必须满足恒为半正定矩阵。
常用的核函数有如下几种:
| 核函数 | 表达式 | 说明 |
|---|---|---|
| linear | $\kappa(x,y)={\langle}x,y{\rangle}$ | 计算原始空间的内积 |
| polynomial | $\kappa(x,y)=(\gamma{\langle}x,y{\rangle}+c)^{d}$ | 计算d维空间的内积 |
| Radial Basis Function | $\kappa(x,y)=exp(-\gamma\vert{x-y}\vert^{2})$ | - |
| sigmoid | $tanh(\gamma{\langle}x,y{\rangle}+c)$ | - |
软间隔SVM
注意:软间隔相当于SVM的正则化
到目前为止,以上讨论都是假设SVM在原始空间或者高维空间将数据集完全线性分割开来,但是将数据完美的线性分开是否会产生或拟合?由此引出软间隔SVM。先前讨论的SVM约束条件为:
\[y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1\]这表示的是所有样本都在该类对应的支持向量的外侧,那么,现在允许一定数量的样本不在外侧,而在内侧,需要满足的条件变为:
\[y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1-\xi_{i}\]其中$\xi$为松弛变量。显然,这个变量不能过大,否则约束就无意义了,需要对它进行限制,将其加入到最小化目标函数中,原SVM的优化问题就变成了:
\[\begin{aligned} min \ \frac{1}{2}||\theta||_{2}+C\sum_{i=1}^{m}\xi_{i}, \qquad s.t.& \ y^{(i)}(x^{(i)}\theta^{T}+\theta_{0})\ge1-\xi_{i},i=1,...m \\ & \ \xi_{i}\ge0,i=1,...m \\ \end{aligned}\]其中$C$为权衡系数,其值越大对松弛变量的约束越大。此时的拉格朗日函数变为:
\[\begin{aligned} \max\limits_{\lambda,\gamma}\ \min\limits_{\theta,\xi} L(\theta,\xi,\lambda,\gamma)&=\frac{1}{2}||\theta||_{2}^{2}+C\sum\limits_{i=1}^{m}\xi_{i}-\sum_{i=1}^{m}\lambda_{i}(y^{i}\cdot{}x^{i}\theta^{T}+y^{i}\theta_{0}-1+\xi_{i})-\sum_{i=1}^{m}\gamma_{i}\xi_{i} \end{aligned}\]令$\frac{\partial{L}}{\partial{\theta}}=\frac{\partial{L}}{\partial{\theta_{0}}}=\frac{\partial{L}}{\partial{\xi_{i}}}=0$得:
\[\left\{ \begin{aligned} &\theta^{*}=\sum_{i=1}^{m}\lambda_{i}y^{i}x^{i} \\ &-\sum\limits_{i=1}^{m}\lambda_{i}y^{i}=0 \\ &C=\lambda_{i}+\gamma_{i} \\ \end{aligned} \right.\]将最优$\theta^{*}$带入得:
\[\begin{aligned} L(\lambda,\xi)&=\frac{1}{2}||\theta^{*}||_{2}^{2}+\lambda_{i}\sum_{i=1}^{m}\xi_{i}+\gamma_{i}\sum_{i=1}^{m}\xi_{i}-\sum_{i=1}^{m}\lambda_{i}y^{i}x^{x}{\theta^{*}}^{T}+\sum_{i=1}^{m}\lambda_{i}-\sum_{i=1}^{m}\lambda_{i}\xi_{i}-\sum_{i=1}^{m}\gamma_{i}\xi_{i} \\ &=\frac{1}{2}\theta^{*}{\theta^{*}}^{T}-(\sum_{i=1}^{m}\lambda_{i}y^{i}x^{i})\cdot{\theta^{*}}^{T}+\sum_{i=1}^{m}\lambda_{i} \\ &=\sum_{i=1}^{m}\lambda_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}\lambda_{j}y^{i}y^{j}x^{i}{x^{j}}^{T} \end{aligned}\]可以看到需要最大化的目标函数是一样的,只不过多了一个约束项$C=\lambda_{i}+\xi_{i}$,完整写出来如下所示:
\[\begin{aligned} \max\limits_{\lambda}\ L(\lambda)&=\sum_{i=1}^{m}\lambda_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}\lambda_{j}y^{i}y^{j}x^{i}{x^{j}}^{T} \\ s.t. \ & 0\le\lambda_{i}\le{C}, \ \sum\limits\lambda_{i}y^{i}=0 \end{aligned}\]SVM的具体优化算法请参阅SMO一章,实现指导也在那一章。这里只放出完整代码:完整代码
SVR
(待补充)
SVM V.S. LR
SVM与LR是经常被用来比较的一对模型。
首先,从数学形式上来作对比,然后再去探究背后的根源。对于机器学习模型而言,最核心的部分就是其损失函数或目标函数,该函数决定了算法的目的与优化方法。
LR的损失函数为:
\[\begin{aligned} Loss_{LR}&=\sum_{i}[y\ln\frac{1}{\hat{y}}+(1-y)\ln\frac{1}{1-\hat{y}}] \\ &=\sum_{i}[-y*x\theta^{T}+ln(1+e^{x\theta^{T}})] \\ \end{aligned}\]SVM的损失函数为:
\[\begin{aligned} Loss_{SVM}&=\frac{1}{2}||\theta||_{2}+\sum\limits_{i}max(0,1-y\hat{y}) \\ &=\frac{1}{2}||\theta||_{2}+\sum\limits_{i}max(0,1-y(x\theta+\theta_{0})) \\ \end{aligned}\]不难发现,SVM中的$max(0,1-y\hat{y})$项,在$y\hat{y}{\ge}1$时为0,即SVM实际上对正确分类的样本是不计入loss的。而反观LR,不难发现LR在数学形式上的loss是无法取得$0$值的,这是因为sigmoid函数的性质就不允许模型精确地输出${0,1}$值,理论上只有在无穷远处才能取得。可以假设一个存在离群点的场景,若SVM对该离群点已能正确分类,那么在训练时就不会再将该点考虑进去,而LR则会收该离群点的影响。所以可以看出,SVM对离群点的抗性要高于LR。而且,LR的决策边界会受两个类别样本分布的影响,而SVM则不会,其决策边界只受支持向量的影响。
同时还在损失函数中发现,SVM自带L2正则项,LR则不带。
然后,两者的出发点就不同。LR是从概率的思想出发,使用一个线性回归去拟合正反事件的对数机率;而SVM的思想是启发性的,直接学习一个最大间隔超平面去将两个类别分开。
然后再看两者的输出函数,LR的预测函数:
\[\begin{aligned} \hat{y}_{LR}&=\frac{1}{1+e^{-x\theta^{T}}} \\ \end{aligned}\]SVM的预测函数:
\[\begin{aligned} \hat{y}_{SVM}&= \left\{ \begin{aligned} &+1, &\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}\langle\hat{x},x^{i}\rangle\ge+1\\ &-1, &\sum_{i=1}^{m}\lambda_{i}^{*}y^{i}\langle\hat{x},x^{i}\rangle\le+1\\ \end{aligned} \right. \end{aligned}\]由于SMV的预测函数中存在两训练样本的内积项,所以核技巧能很自然而然的与SVM相结合;除了这个原因之外,SVM中的拉格朗日参数$\lambda$,非支持向量的该参数值是为$0$的,所以在计算决策边界时的计算量并不高,这也是核技巧常用于SVM的原因之一。
最后,两者的优化复杂度不一样,LR由于模型本身简单,可以使用迭代的梯度下降法进行优化;而SVM目前成熟的优化方法就是SMO算法。另外,由于SVM使用了“距离”的概念,所以对数据做归一化处理是有好处的,还由于维度诅咒的原因,在高维空间下距离的概念会变得十分抽象,所以在高维情况下,会更倾向于实用LR。
关于对偶问题
至于为什么要将SVM的原问题转化成对偶问题,在网上搜到有如下几种说法:
- 对偶问题的解中有$\langle\hat{x},x^{i}\rangle$这样的内积形式,可以很方便地引入核技巧
- 从对偶问题的求解过程可以看出只需要求出最优的$\lambda^{}$即可,而$\lambda$的数量等同于样本的数量,但是非支持向量对应的$\lambda_{i}^{}$均为零,所以真正要求解的$\lambda$数量并不多;反之,原问题需要求解$\theta^{}$,而$\theta^{}$的数量等同于数据的维度。